고정 헤더 영역
상세 컨텐츠
본문
Partitioning
n개의 개체를 k개의 클러스터로 분할하고 선택한 분할 기준을 최적화한다.
global optimal solution을 찾으려면 k^n개의 파티션을 검사해야 한다. 하지만 이것은 너무 비싸기 때문에 가능한 모든 부분 집합 중 작은 부분 집합만 고려하는 heuristic methods를 사용해야 한다.
한 클러스터의 제곱 오차 공식은 아래와 같다.
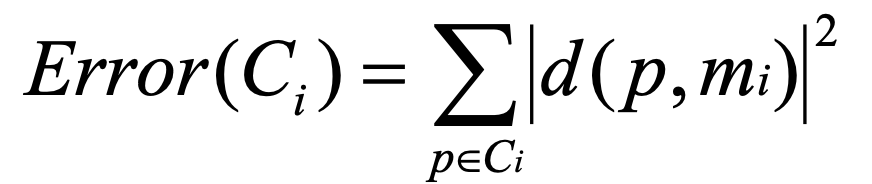
모든 클러스터의 제곱 오차 공식은 아래와 같다.
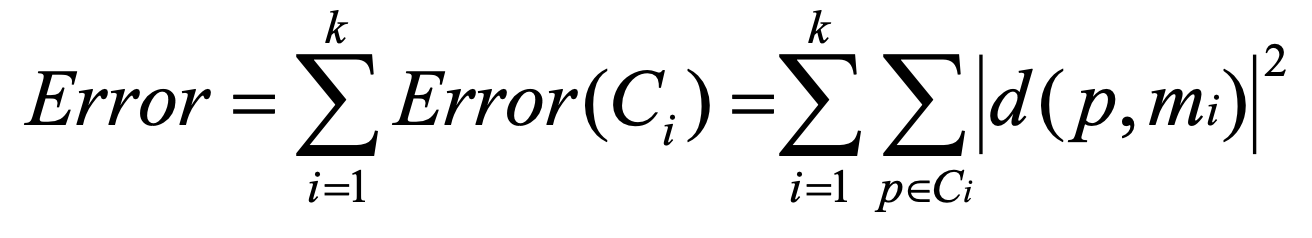
아래 그림은 클러스터 i의 오차를 계산한 것이다.
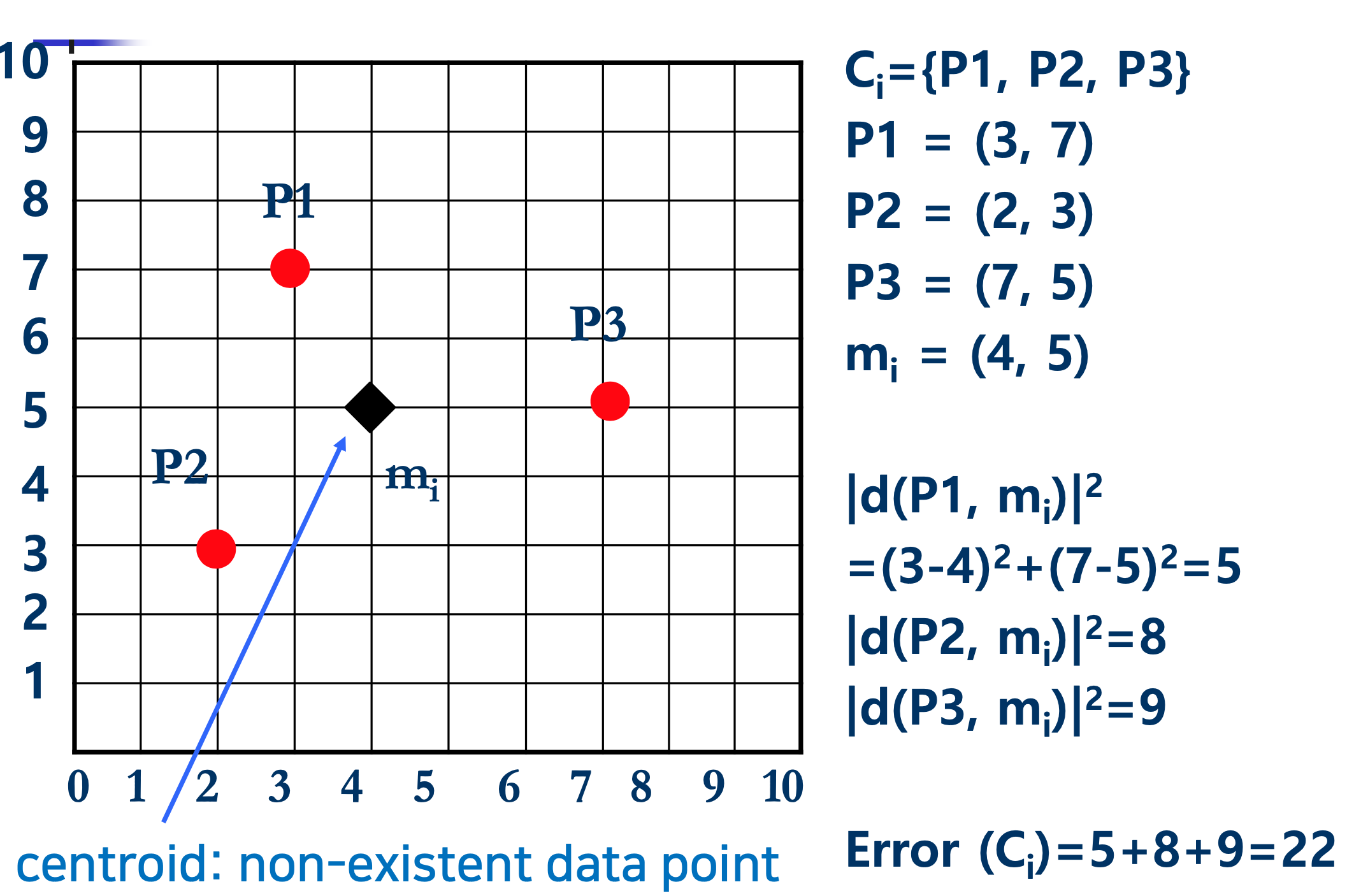
1. K-means
- k-means Algorithm
◼ k개의 개체를 초기 클러스터로 임의로 선택
◼ 클러스터가 변경되지 않을 때까지 반복
◼ 각 개체 Oi에 대해
◼ Oi와 k 중심체 사이의 거리 계산
◼ 중심점이 Oi에 가장 가까운 클러스터에 Oi 할당
◼ 현재 할당을 기반으로 클러스터 중심 업데이트
- Strength of k-means
◼ 대규모 데이터셋에 대해 비교적 효율적
◼ O(tkn) (n 은 객체의 수, k는 클러스터의 수, t는 반복의 수이다. 일반적으로 k, t <<n)
- Weakness of k-means
◼ 평균을 정의할 수 있는 경우에만 적용된다. (범주형 데이터에는 적용되지 않는다.)
◼ 노이즈가 많은 데이터 및 특이치를 처리할 수 없다.
◼ k(군집 수)를 지정해야 함
- Variations of k-Means Algorithm
◼ 초기 k 중심체 선택
◼ 거리 측정
◼ 군집 평균을 계산하기 위한 전략
2. K-modes
군집 평균을 mode로 바꾼다.
통계학에서 집합의 mode는 다음과 같다.
e.g. 집합 {a, b, a, a, c, b}의 모드가 가장 빈도가 높은 값 a이다(mode가 둘 이상 있을 수 있음).
아래 그림은 mode vector를 구한 하나의 예시이다.
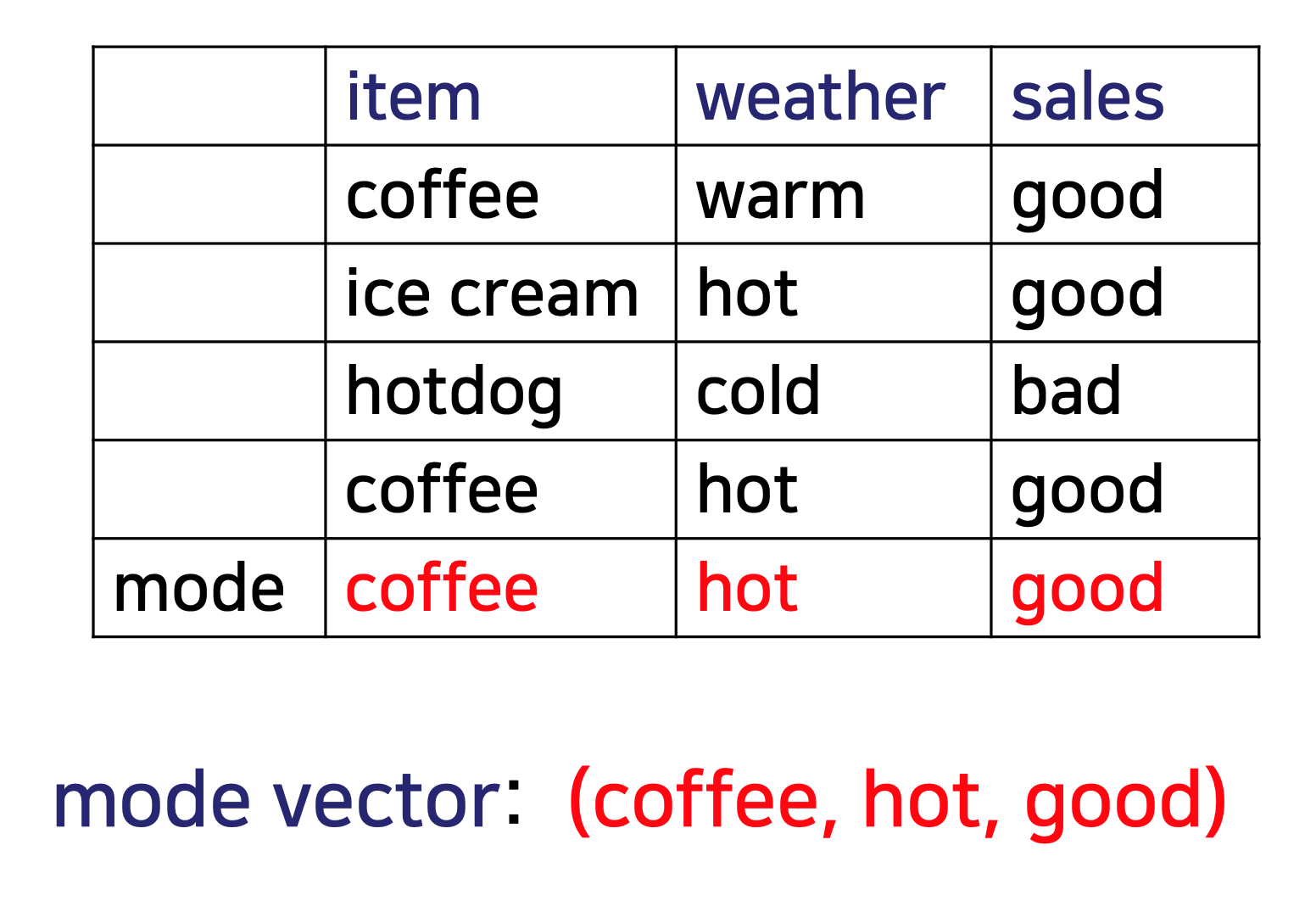
k-modes 클러스터링에서 클러스터 중심은 mode vector로 표시된다.
클러스터의 mode vector는 클러스터의 각 객체와 클러스터 중심 사이의 거리의 합을 최소화한다.
- k-modes Algorithm
Step1
◼ k개의 고유 개체를 초기 군집으로 랜덤하게 선택
Step2
◼ 각 객체와 군집 모드 벡터 사이의 거리를 계산
◼ 중심에서 개체까지의 거리가 가장 짧은 클러스터에 개체를 할당
◼ 모든 개체가 클러스터에 할당될 때까지 이 단계를 반복
Step3
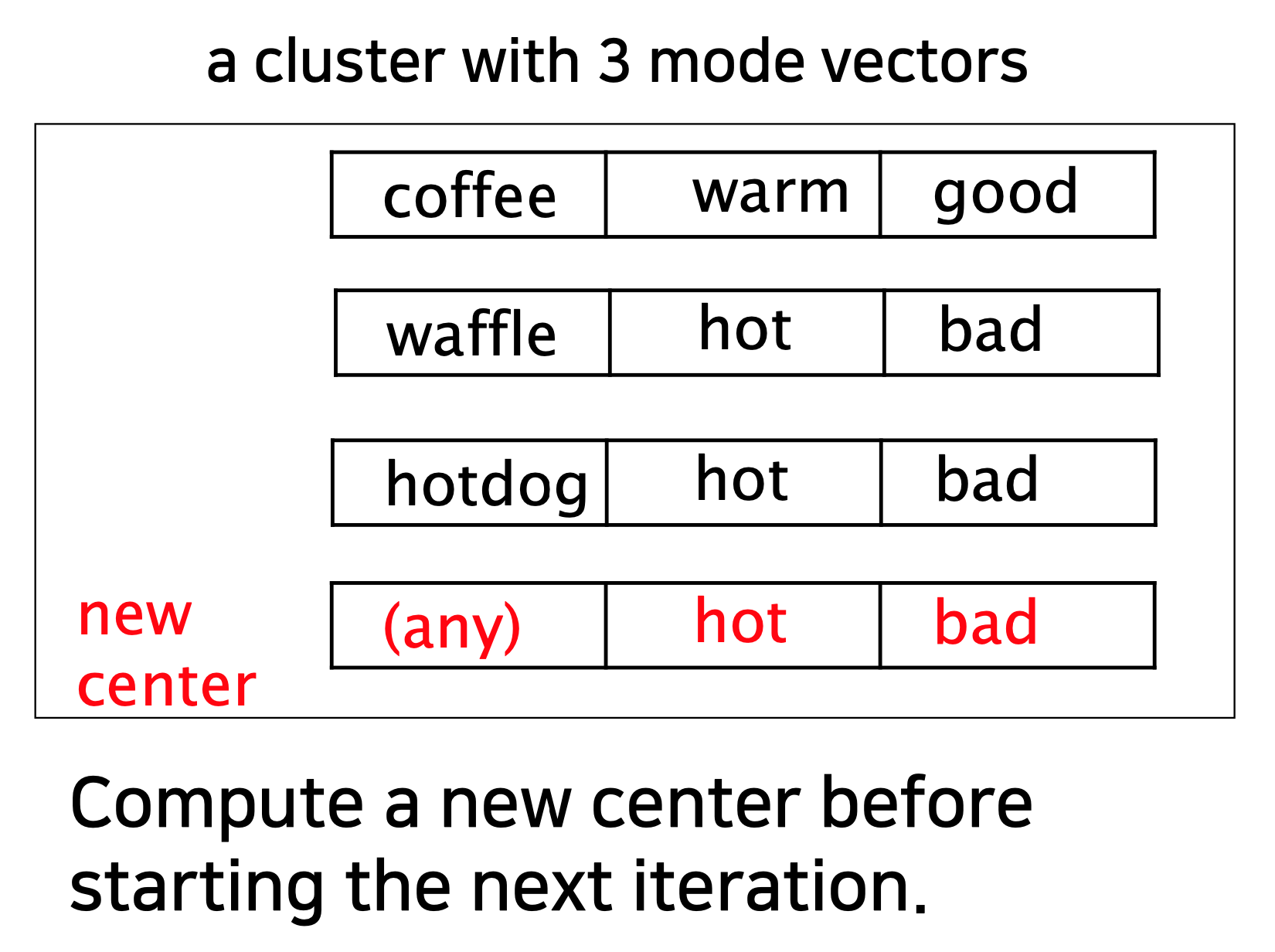
◼ 각 클러스터에 대한 새 모드 벡터를 선택하고 이전 모드 벡터와 비교
◼ 다를 경우 2단계로 다시 이동하고, 그렇지 않을 경우 중지
k-modes에서 거리 구하는 공식은 아래와 같다.

아래 그림은 위 공식을 이용해 mode vector 사이의 거리를 구하는 예시이다.

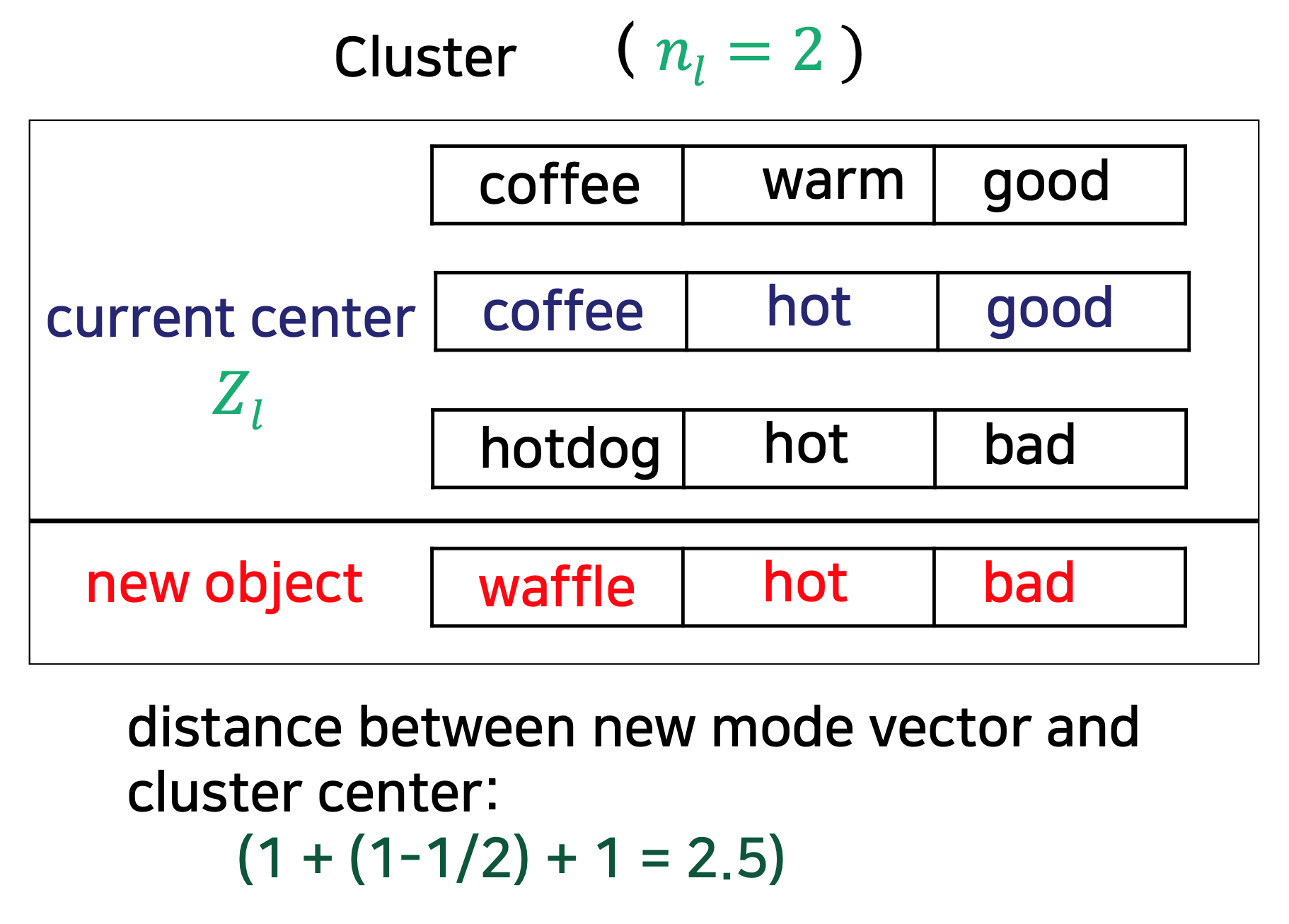
cluster center에서의 거리 구하는 법은 아래와 같다.

아래 그림은 위 공식을 이용해 mode vector와 cluster center 사이의 거리를 구하는 예시이다.
클러스터링 프로세스는 다음과 같은 목적 함수를 최소화한다.
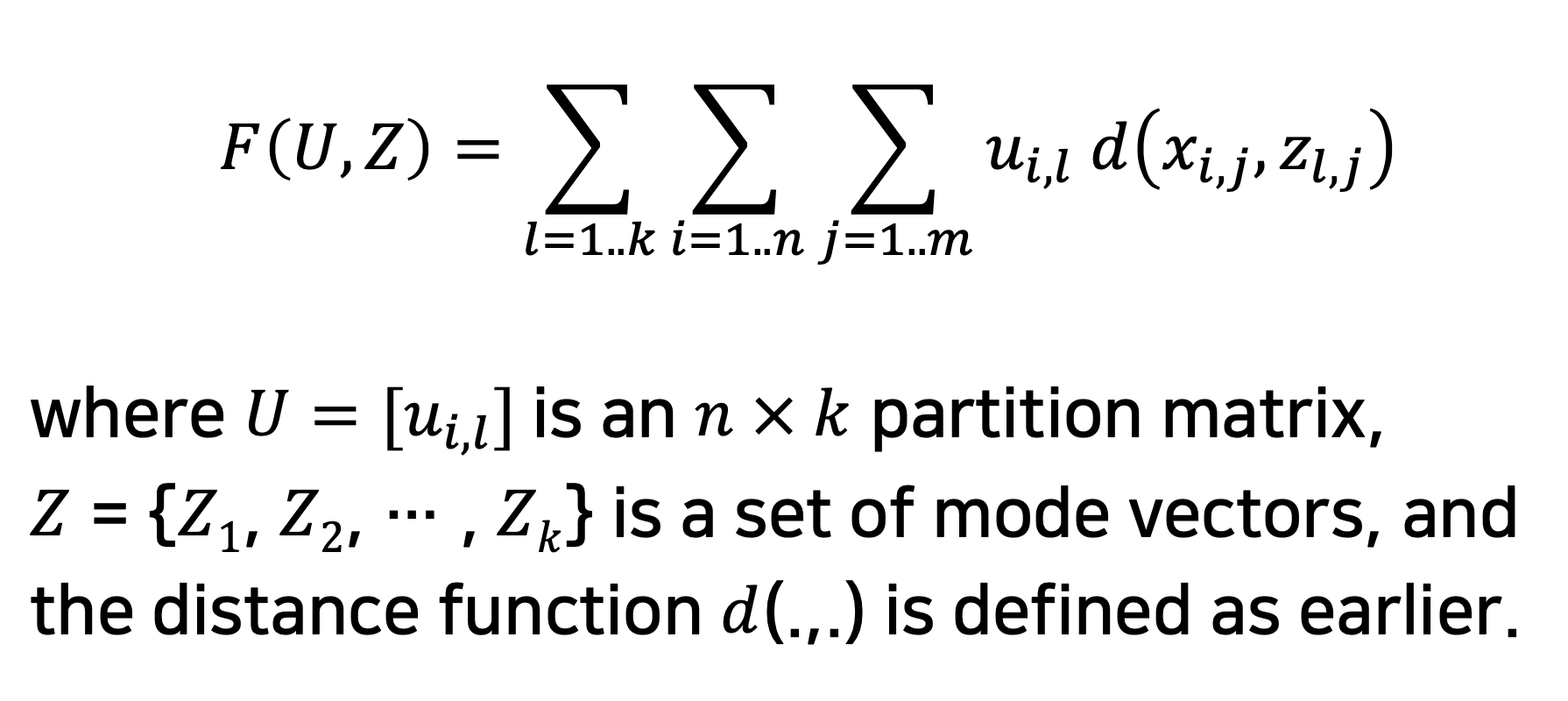
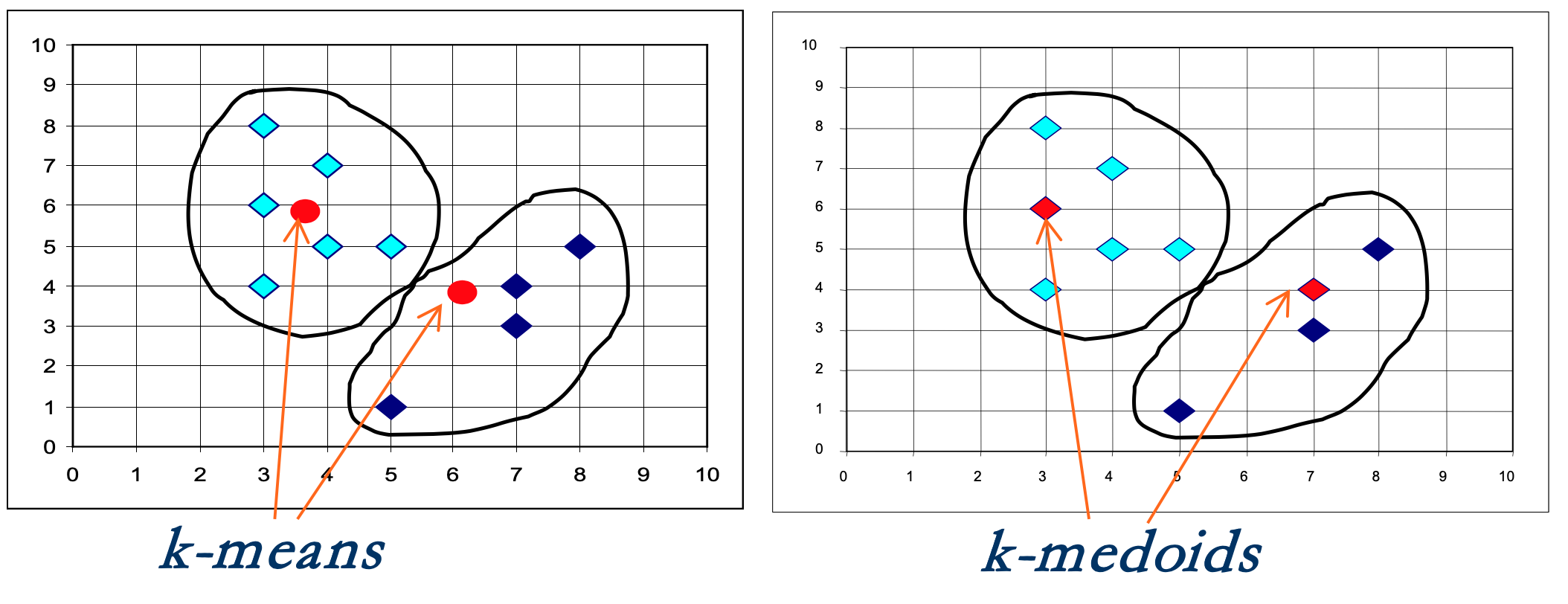
3. K-medoids
medoids라고 하는 k개의 대표 객체를 찾는다.
1) PAM
- PAM Algorithm
◼ k개의 객체를 초기 medoid로 임의로 선택
◼ 클러스터에서 변경이 없을 때까지 반복
◼ 가장 가까운 메도이드를 사용하여 각 개체를 클러스터에 할당
◼ medoid가 아닌 개체를 임의로 선택
◼ medoid를 교체하는 데 드는 총 비용을 계산
◼ 교환하고 비용이 절감되면 medoid를 교체
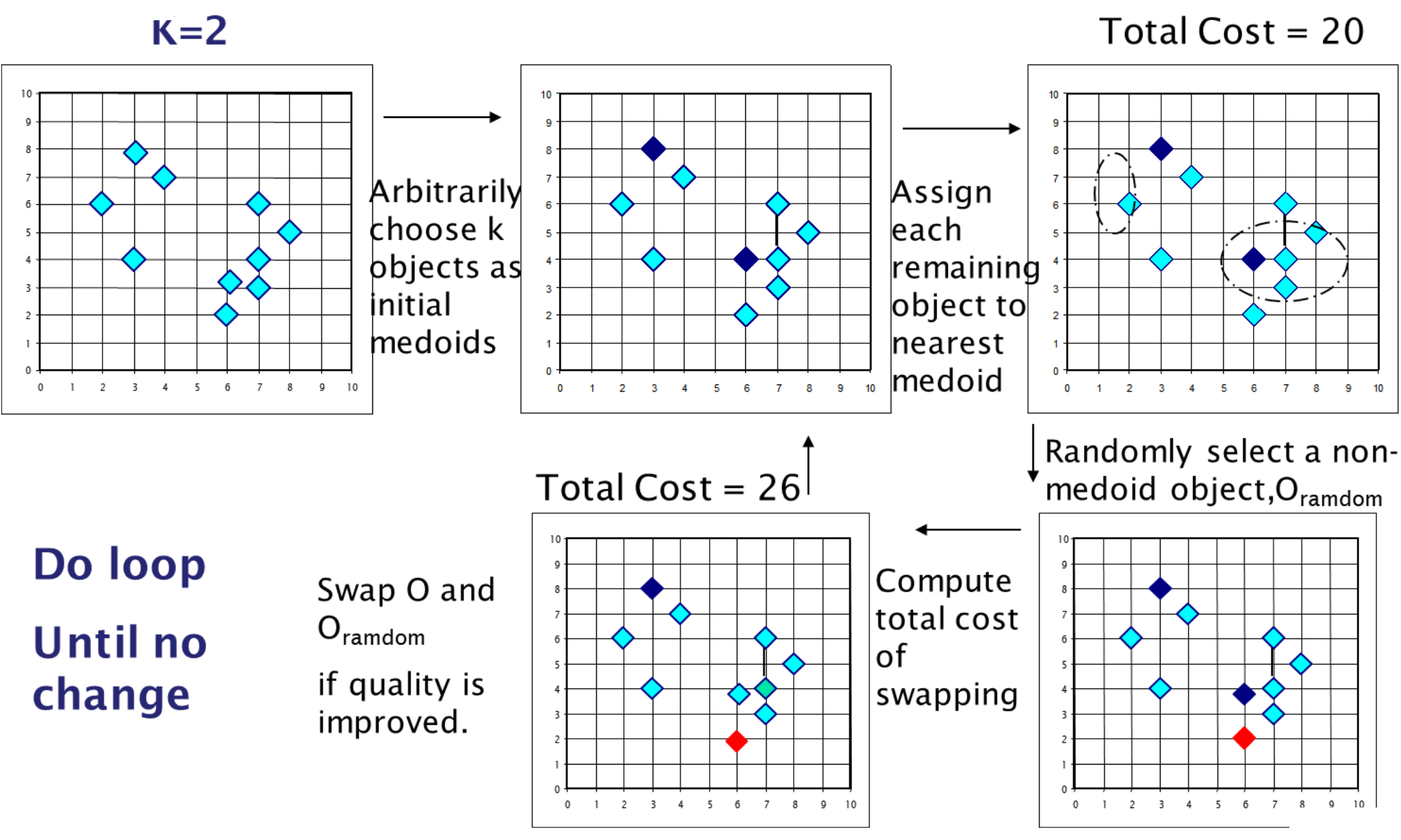
위 알고리즘에서 medoid를 교체하는 비용은 아래와 같이 계산한다.

- strength and weakness of PAM
◼ medoid는 평균보다 특이치나 다른 극단값의 영향을 덜 받기 때문에 PAM은 특이치가 있을 때 k-means보다 더 강하다.
◼ PAM은 소규모 데이터 세트에는 효율적으로 작동하지만 대규모 데이터 세트에는 잘 확장되지 않는다.
◼ 각 반복에 대한 O(k(n-k)^2) (n은 데이터 개체의 수이고, k는 클러스터의 수)
◼ CLARA와 CLARANS가 medoid를 더 빨리 찾는다.
2) CLARA
◼ CLARA는 데이터 세트의 여러 랜덤 샘플을 그리고, 각 샘플에 PAM을 적용하며, 최고의 클러스터링을 출력으로 제공한다.
◼ 전체 데이터 세트에서 PAM이 완전히 계산되는 것을 방지한다.
◼ PAM보다 큰 데이터 세트(예: 10개 클러스터의 1,000개 개체)를 처리할 수 있다.
◼ 효율성과 효과는 표본 추출에 따라 달라진다.
◼ CLARA는 S+와 같은 통계 분석 패키지에 내장되어 있다.
- CLARA Algorithm
◼ 최소 비용 설정
◼ q번 반복하기
◼ 표본 데이터 집합 D에서 랜덤하게 객체를 그려 표본 S 생성
◼ PAM 알고리즘을 적용하여 S에서 M 메도이드 집합 생성
◼ 비용 계산(M,D)
◼ 비용(M, D) < 최소 비용인 경우
{최소 비용 = 비용(M, D);
bestset = M;}
-weakness of CLARA
◼ 효율성이 표본 크기, 표본 수 및 표본 품질에 따라 달라진다.
3) CLARANS
CLARA처럼 전체 데이터 세트 대신 샘플을 사용한다. 각 샘플에 대해 많은 노드를 생성한다. (노드는 k-medoid 집합)
(예: 아래 다이어그램의 빨간색 다이아몬드 2개)
노드를 검색하여 medoid를 다른 medoid와 교환하여 총 비용을 절감할 수 있는 기회를 찾는다.
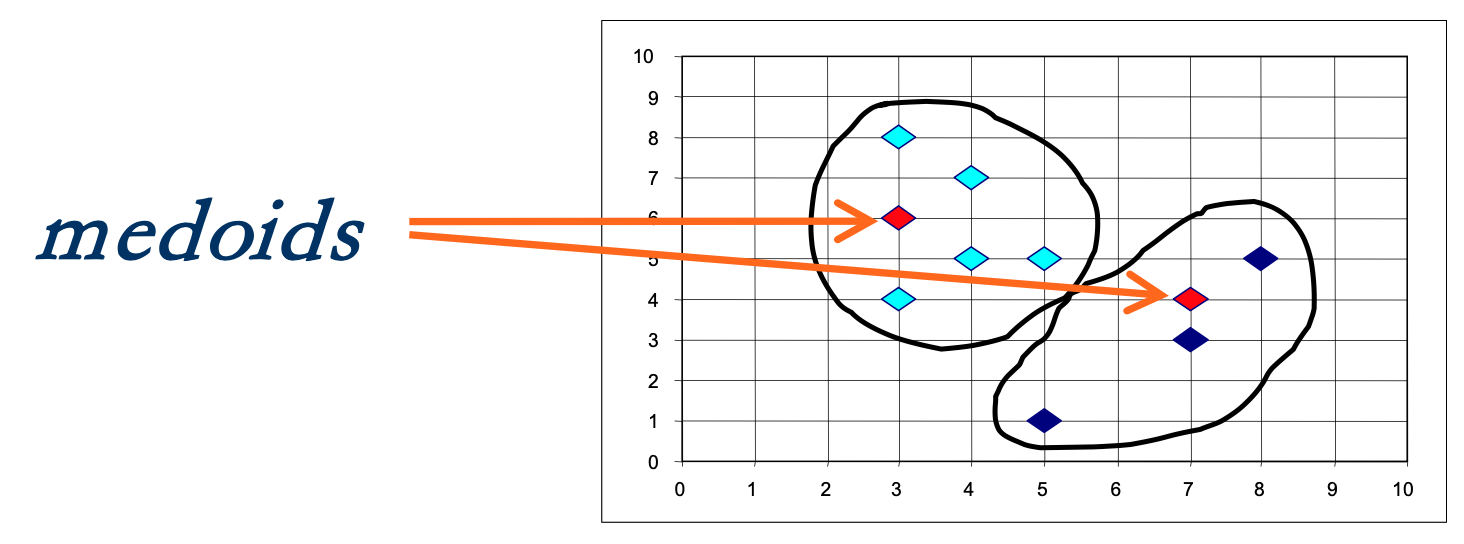
- CLARANS Algorithm
◼ k 데이터 점을 초기 k-medoid로 선택
◼ 임의의 medoid x(현재 medoid라고 함)를 선택
◼ medoid max_neighbors만큼 다음 검색을 반복
◼ k-medoid 중 하나가 아닌 현재 medoid의 임의 이웃을 선택
◼ 현재 메도이드를 교체해야 하는지 여부를 결정
◼ 만약 이웃이 총비용을 낮추면, 그것이 새로운 medoid
◼ 그렇지 않으면 현재 노드가 로컬 최적 상태로 유지
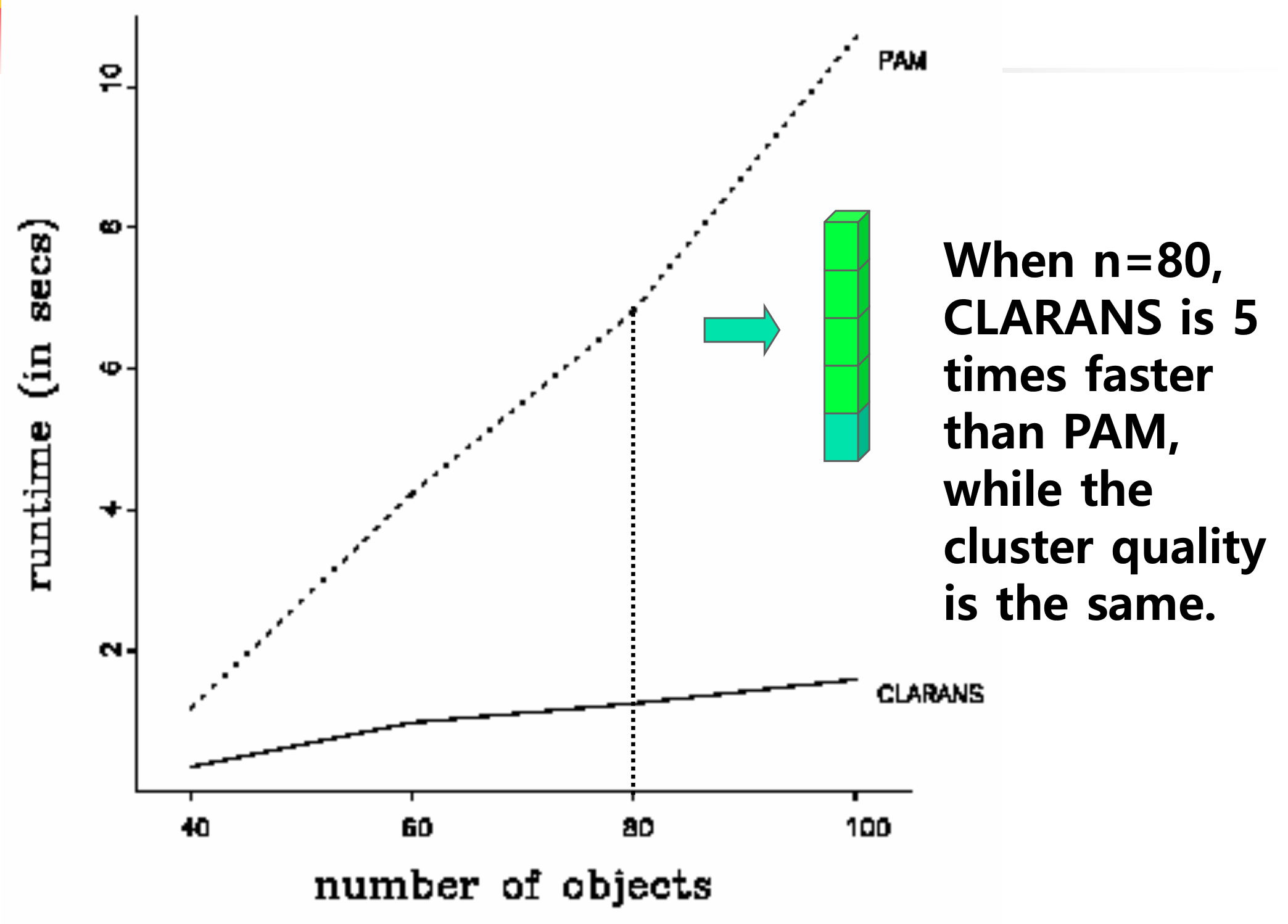
- CLARANS vs PAM
◼ 대규모 및 중간 규모의 데이터셋의 경우 CLARANS는 PAM보다 효율적이다.
◼ 소규모 데이터 세트의 경우 CLARANS의 능률이 PAM을 크게 능가한다.
-CLARANS vs CLARA
◼ CLARANS는 CLARA보다 더 좋은 클러스터를 찾는다.
◼ CLARANS CLARA보다 훨씬 더 많은 시간을 사용할 수 있다.
◼ 사용 시간이 같을 때 클라라보다 CLARANS가 더 낫다.
'machine learning' 카테고리의 다른 글
| [ML] Clustering Algorithms – DBSCAN (0) | 2022.12.15 |
|---|---|
| [ML] Clustering Algorithms –Expectation-Maximization (Gaussian Mixture Model) (0) | 2022.12.15 |
| [ML] Clustering Algorithms – Clustering Quality Measure (2) | 2022.12.14 |
| [ML] Classification Algorithms – Support Vector Machine (0) | 2022.12.13 |
| [ML] Classification Algorithms – Logistic Regression (0) | 2022.12.13 |





댓글 영역