고정 헤더 영역
상세 컨텐츠
본문 제목
[ML] Clustering Algorithms –Expectation-Maximization (Gaussian Mixture Model)
본문
EM
EM은 통계 모델에서 매개 변수의 최대 가능성을 찾기 위한 반복적인 방법으로, 모델은 숨겨진(잠재적) 변수에 의존한다.
-EM Algorithm
◼ expectation(E) 단계와 maximization(M) 단계를 번갈아 수행하면서 반복
◼ (E) 단계는 모수에 대한 현재 추정치를 사용하여 평가되는 log-likelihood의 기대 함수를 생성
◼ (M) 단계는 (E) 단계에서 발견되는 예상 log-likelihood를 최대화하는 모수를 계산
◼ 이러한 모수 추정치는 다음 (E) 단계에서 숨겨진 변수의 분포를 결정하는 데 사용
- Hidden Parameter Problem and Solution
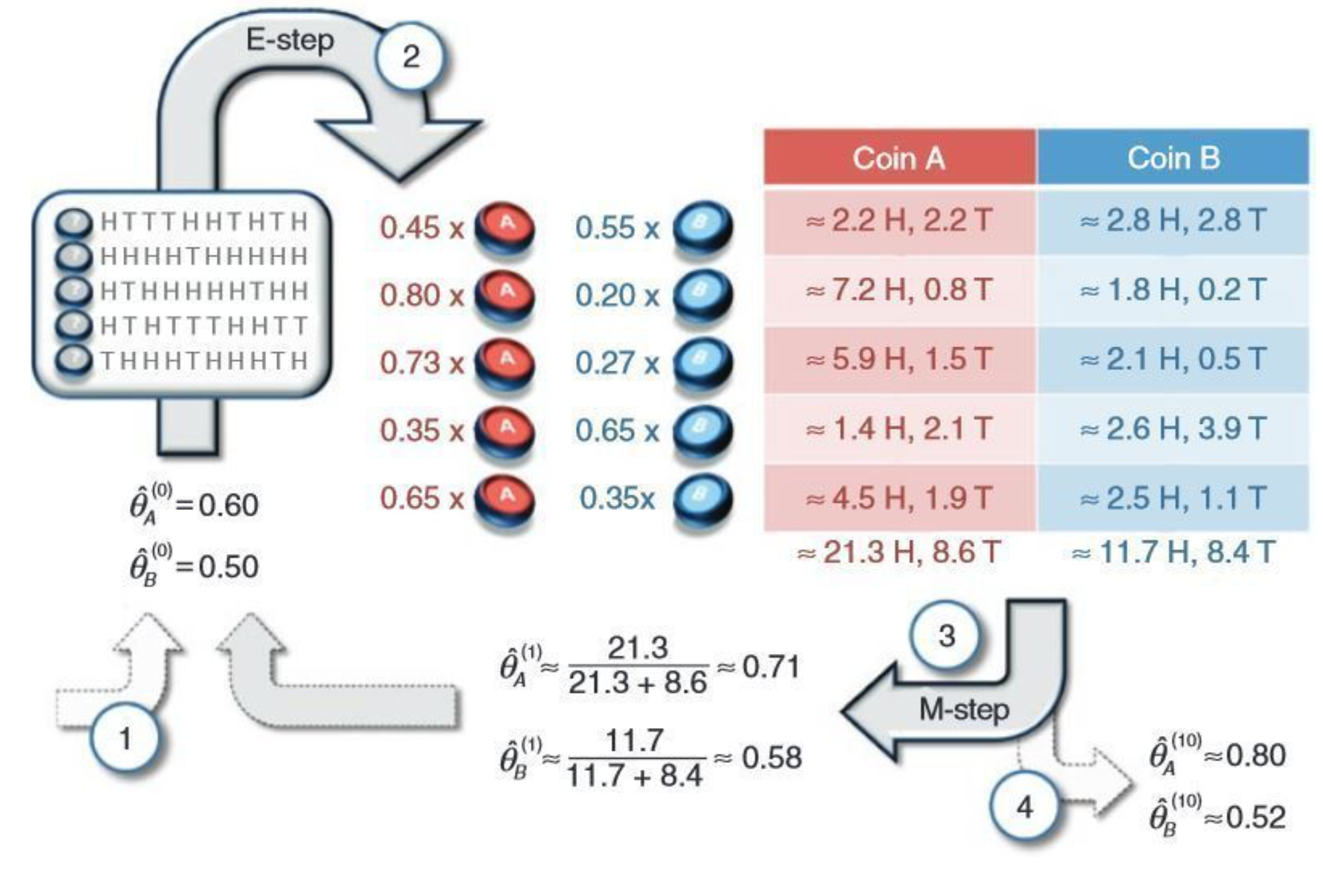
◼ 변수가 숨겨져있을 때 각 변수가 똑같이 선택될 가능성이 있다면 우리는 알려지지 않은 매개변수 'p'와 'q'를 추정할 수 있는가?
=> 우리는 EM 알고리즘을 채택하여 문제를 반복적으로 해결할 수 있다.
∙ E (기대) 단계
◼ p와 q 값에 대한 초기 추측으로 시작
◼ 확률이 'x'인 코인 A에서 나올 수 있고 확률이 '1-x'인 코인 B에서 나올 수 있다고 말할 것이다.
◼ 각 동전에서 예상되는 앞면과 뒷면의 수를 계산
∙ M(최대화) 단계
◼ (MLE 계산과 유사한) 'E' 단계에서 각 코인의 예상 앞면과 뒷면 수에 대한 log-likelihood를 계산
◼ 알 수 없는 매개 변수의 log-likelihood를 최대화하고 각 코인에 대해 log-likelihood가 최대화되는 p와 q의 새 값을 다시 추정
-Walkthrough Example

Applying EM to Clustering
- Problems of K-means clustering and Solution(EM Clustering)
◼ 클러스터 중심까지의 거리를 항상 구형으로 가정한다. (hard clustering으로 이어지지만 항상 정답은 아니다.)
◼ greedy algorithm으로 최적이 아닐 수 있다.
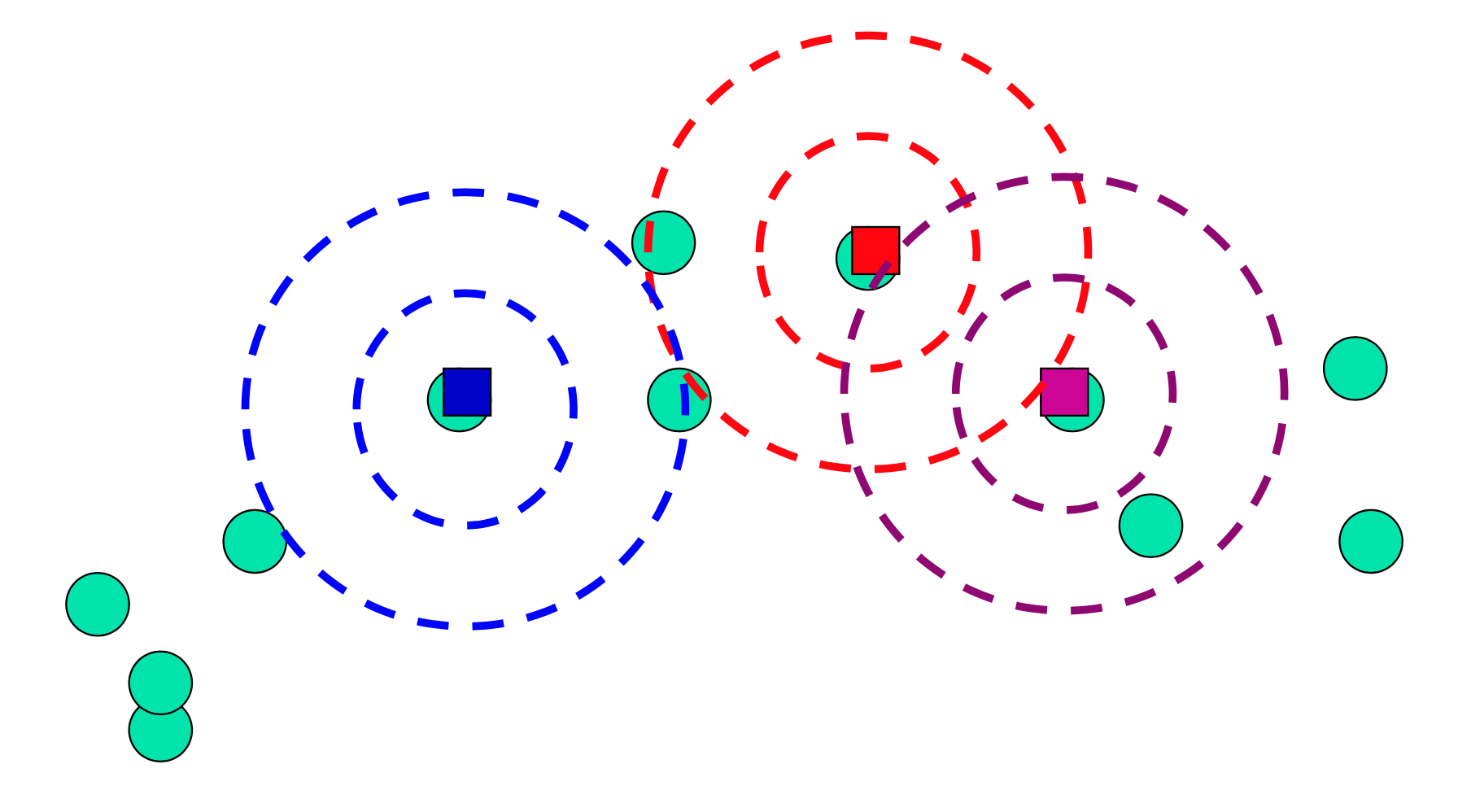
=> EM Clustreing은 타원형 클러스터를 가정(soft clustering이며, 특정 확률로 클러스터에 데이터를 할당)

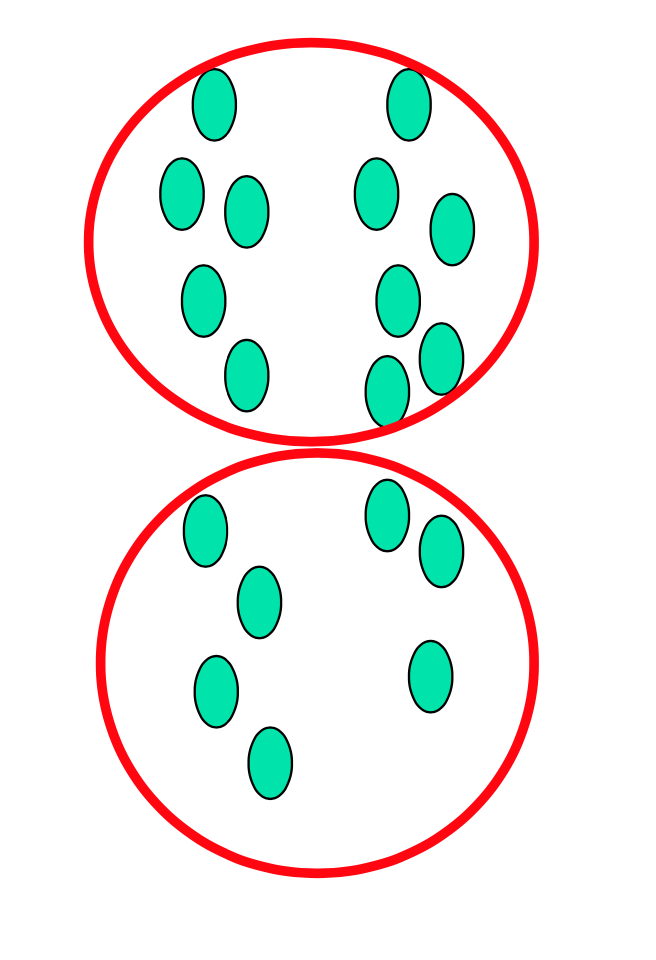
위 그림과 같은 데이터 분포를 가지고 있을 때, k-means는 아래와 같이 hard, spherical한 클러스터링을 하고,
EM은 아래와 같이 soft, elliptical한 클러스터링을 한다.
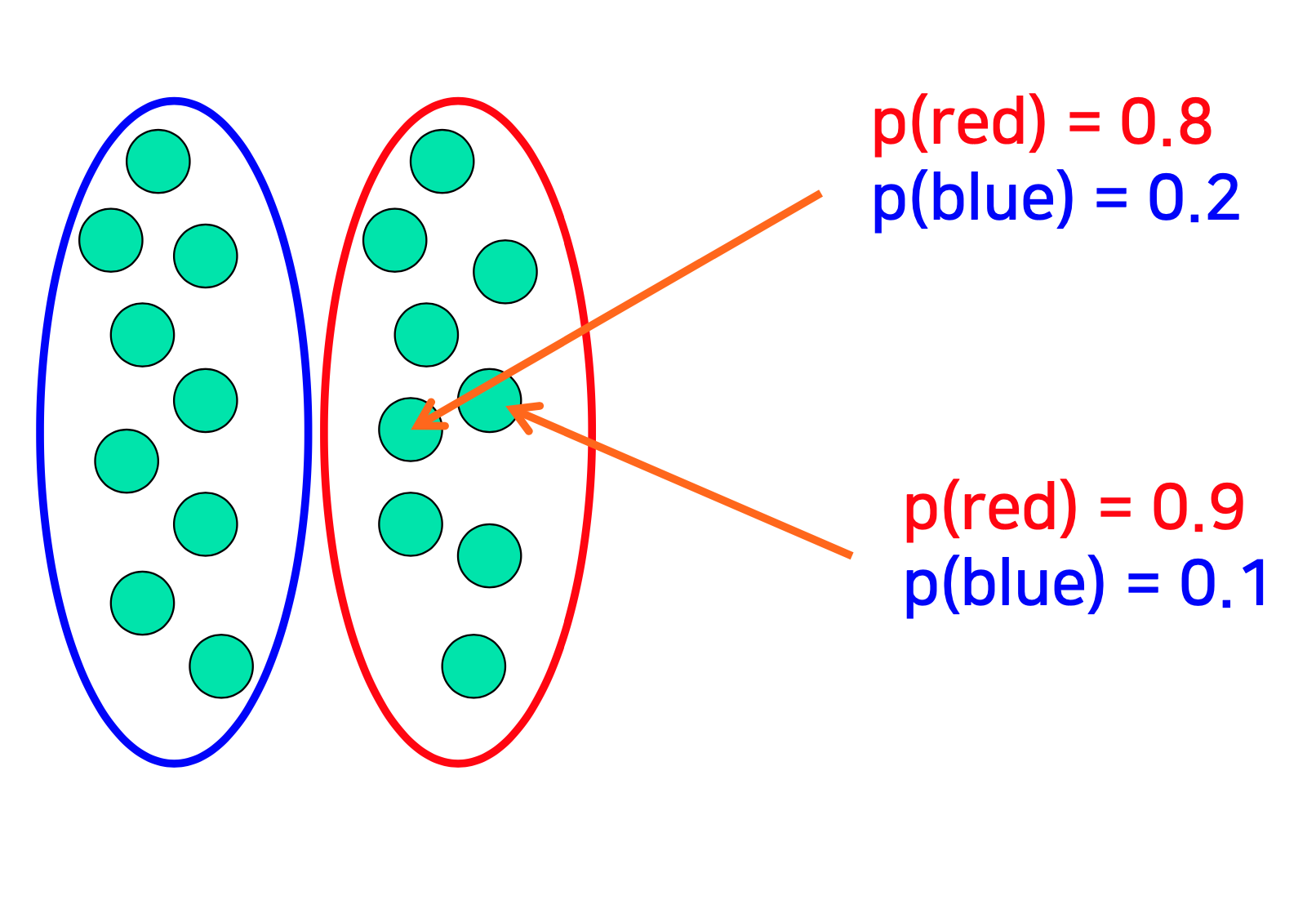
- visualization of EM clustering
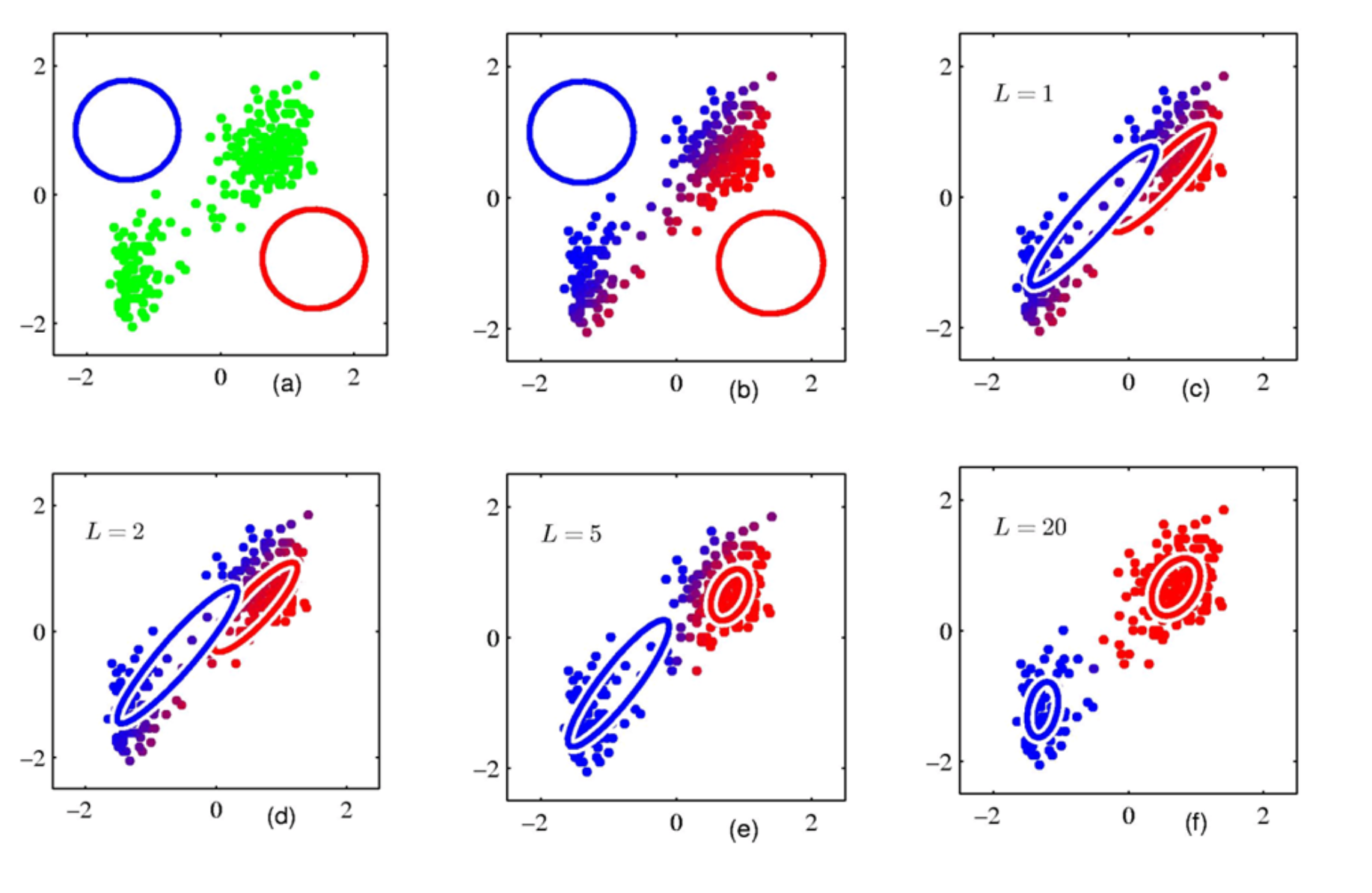
- Advantages of EM clustering
◼ 소프트 클러스터링은 밀도 기반 클러스터링을 어느 정도 확장한다.
- Disadvantages of EM clustering
◼ 매개 변수를 계산하는 데 시간이 오래 걸릴 수 있다.
◼ k를 결정하는 것은 어렵다.
◼ 전역 최소값이 아닌 로컬 최소값을 사용하게 될 수 있다.
-Scikit Learn Support for EM Clustering
import numpy as np
import matplotlib.pyplot as plt import seaborn as sns; sns.set()
from sklearn.mixture import GMM
# generate some data
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting
# create a GMM model and train it
gmm = GMM(n_components=4).fit(X)
# cluster the data
labels = gmm.predict(X)
# plot the clusters
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis');
# After the model has converged, solve the weights, means, and covariances; We can print them out.
print(gmm.means_)
print('\n')
print(gmm.covariances_)'machine learning' 카테고리의 다른 글
| [ML] Classification - SMOTE (0) | 2022.12.16 |
|---|---|
| [ML] Clustering Algorithms – DBSCAN (0) | 2022.12.15 |
| [ML] Clustering Algorithms – Partitioning (0) | 2022.12.15 |
| [ML] Clustering Algorithms – Clustering Quality Measure (2) | 2022.12.14 |
| [ML] Classification Algorithms – Support Vector Machine (0) | 2022.12.13 |





댓글 영역