고정 헤더 영역
상세 컨텐츠
본문
Clustering Quality Measure
1. Elbow Method
◼ K-Means Clustering 분석 결과에 적용된다.
◼ k의 후보 값 범위를 선택한 다음 K-Means를 적용한다.
◼ 군집에서 중심까지의 점의 평균 거리를 찾고 그래프로 나타낸다.
◼ 평균 거리가 급격히 떨어지는 그래프에서 k 값을 선택한다.
-Picking the "Elbow"

◼ 그래프의 x축은 군집 수(k)이고 y축은 군집 내 중심점과 데이터 점 사이의 평균 거리이다.
◼ 군집 수(k)가 증가하면 평균 거리가 감소한다.
◼ 최적 군집 수(k)를 찾으려면 거리가 급격히 떨어지는 k값을 찾는다.
◼ "elbow"가 발생하는 지점이 최적의 k이다.
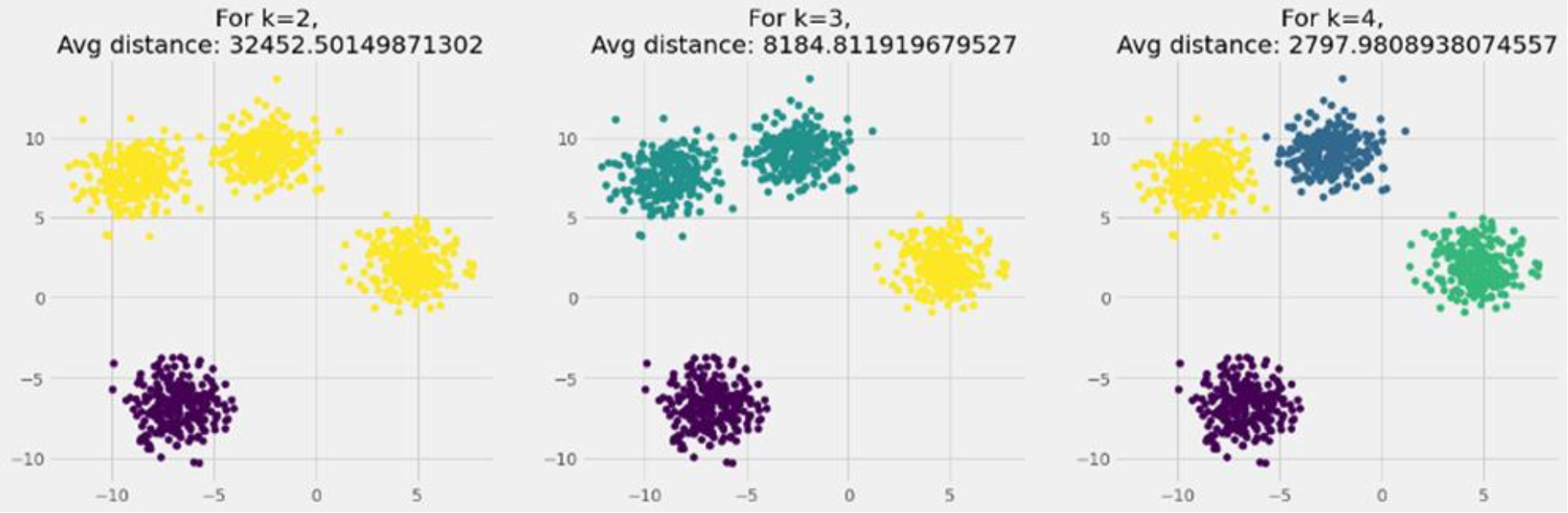
◼ k=2, 3과 4 사이에서 평균 거리가 급격히 떨어진다.
◼ 따라서 k의 최적 값은 4이다.
- python code for Elbow Method
# Using IRIS dataset
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.cluster import KMeans
from sklearn import datasets
iris = datasets.load_iris()
df=pd.DataFrame(iris['data'])
# run K-Means for a range of clusters (k) using a for loop and collecting the distortions into a list
distortions = []
K = range(1,10) for k in K:
kmeanModel = KMeans(n_clusters=k)
kmeanModel.fit(df)
distortions.append(kmeanModel.inertia_)
# plotting the distortions of k-mplt.figure(figsize=(16,8))
plt.plot(K, distortions, 'bx-’)
plt.xlabel('k’)
plt.ylabel('Distortion’)
plt.title('The Elbow Method showing the optimal k’)
plt.show()eans
2. Silhouette Index
◼ K-Means Clustering 분석 결과에 적용된다.
◼ Silhouette index는 물체가 얼마나 유사한지를 나타내는 척도이다.
◼ 모든 표본에 대한 Silhouette index의 평균이다.
◼ 대부분의 개체 값이 높은 경우 클러스터링 구성이 적합하다.
- Steps to find the silhouette coefficient of an i’th point:
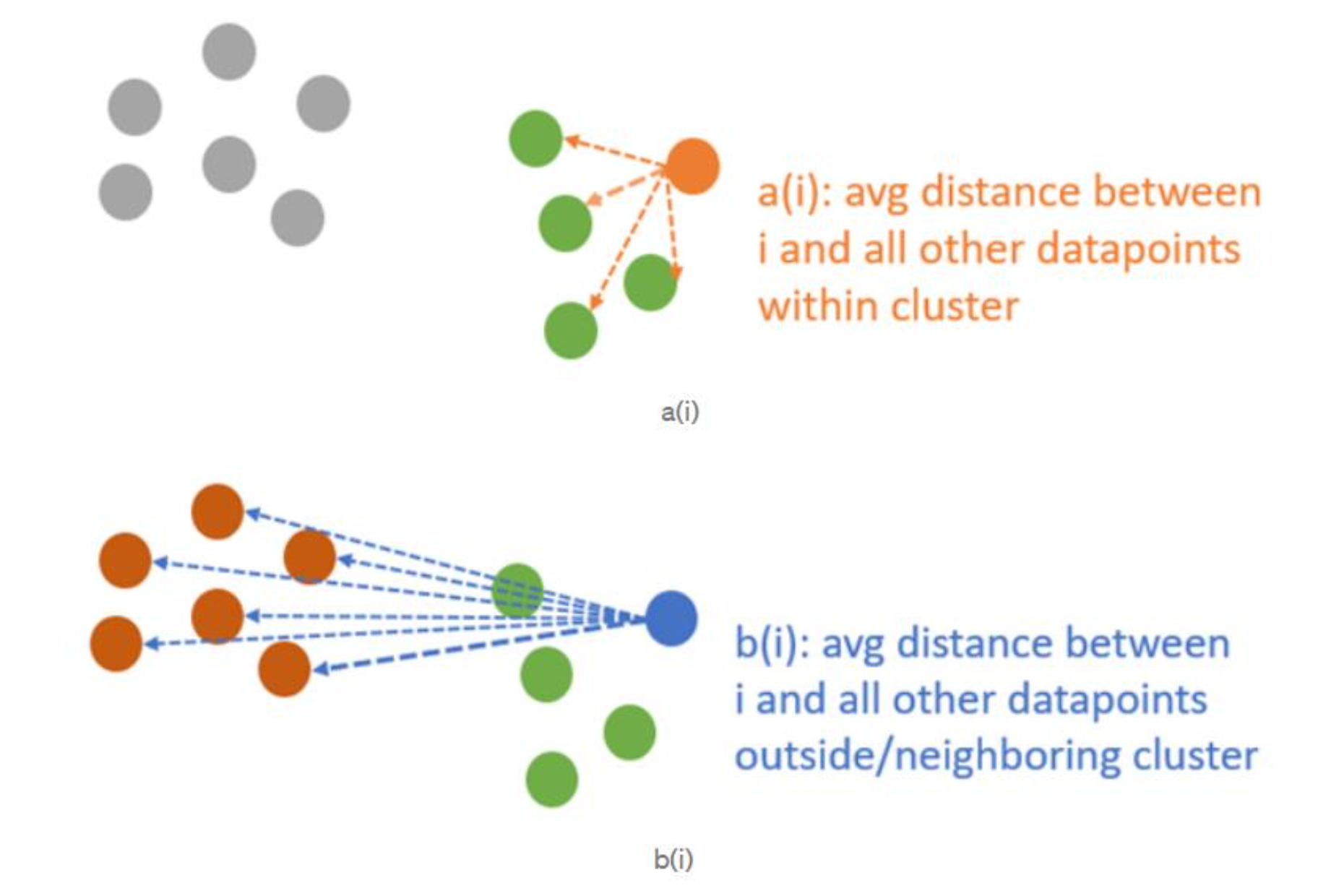
1. a(i): 같은 무리에 있는 다른 모든 점에 대한 해당 점의 평균 거리
2. b(i): 다른 모든 군집의 모든 점에 대한 해당 점의 평균 거리
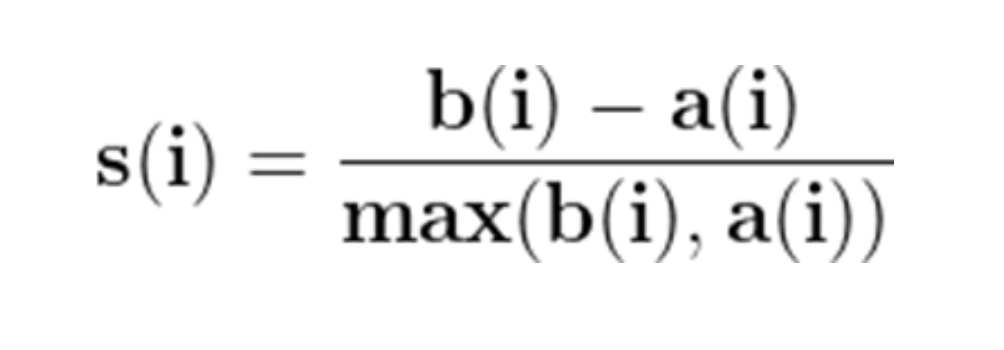
- Computing and Plotting the Average Silhouette Score:
◼ 데이터 세트에서 각 포인트의 silhouette coefficient를 계산한 후 k마다 평균 silhouette 점수를 계산한다.
AverageSilhouette = mean{S(i)}
◼ average silhouette와 K 사이에 그래프를 표시한다. ( 범위는 [-1, 1] )
*important points*
◼ +1은 군집이 서로 멀리 떨어져 있고 명확하게 구분되어 있음을 나타낸다.
◼ 0은 군집이 겹친다는 것을 나타내다.
◼ < 0은 이러한 표본이 잘못된 군집에 할당되었거나 특이치임을 나타낸다.
- Scikit-learn Support for Silhouette Score
from sklearn import datasets
from sklearn.cluster import KMeans
#
# Load IRIS dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
#
# Instantiate the KMeans models
km = KMeans(n_clusters=3, random_state=42)
#
# Fit the KMeans model
km.fit_predict(X)
#
# Calculate Silhouette Score
score = silhouette_score(X, km.labels_, metric='euclidean')
-최적의 "k"를 찾는 방법

◼ Elbow method와 마찬가지로 k의 후보 값 범위(클러스터 수)를 선택한 다음 k의 각 값에 대한 K-Means clustering 분석을 학습한다.
◼ 각 K-Means clustering model에 대해 그림의 silhouette 점수를 나타내고 각 군집의 변동 및 특이치를 관찰한다.
◼ 아래에서 k=4일 때 silhouette 점수가 가장 높고 최적이다.
- Python Code for the Plot
range_n_clusters = [2, 3, 4, 5, 6, 7, 8]
silhouette_avg = []
for num_clusters in range_n_clusters:
# initialize kmeans
kmeans = KMeans(n_clusters=num_clusters)
kmeans.fit(data_frame)
cluster_labels = kmeans.labels_
# silhouette score
silhouette_avg.append(silhouette_score(data_frame,cluster_labels))plt.plot(range_n_clusters,silhouette_avg,’bx-’)
plt.xlabel(‘Values of K’)
plt.ylabel(‘Silhouette score’)
plt.title(‘Silhouette analysis For Optimal k’)
plt.show()
◼ silhouette plot은 cluster_label=1인 군집의 모든 점이 평균 silhouette 점수보다 낮기 때문에 n_cluster 값 3이 잘못된 선택임을 보여준다.
◼ n_cluster 값 5는 잘못된 선택이다. cluster_label=2 및 4인 클러스터의 모든 점이 평균보다 낮은 실루엣 점수이기 때문이다.
◼ n_cluster 값 6은 잘못된 선택이다. cluster_label=1, 2, 4 및 5인 군집의 모든 점이 평균보다 낮은 실루엣 점수이며 특이치도 있기 때문이다.
◼ 2번과 4번 중에서 어떻게 결정해야 할지 명확하지 않다.
◼ n_label=2일 때 cluster_label=1인 클러스터는 세 개의 하위 클러스터가 있기 때문에 하나의 큰 클러스터로 그룹화됩니다.
◼ n_details=4의 경우 모든 그래프의 두께가 비슷하므로 크기가 비슷하므로 최상의 'k'로 간주할 수 있다.
'machine learning' 카테고리의 다른 글
| [ML] Clustering Algorithms –Expectation-Maximization (Gaussian Mixture Model) (0) | 2022.12.15 |
|---|---|
| [ML] Clustering Algorithms – Partitioning (0) | 2022.12.15 |
| [ML] Classification Algorithms – Support Vector Machine (0) | 2022.12.13 |
| [ML] Classification Algorithms – Logistic Regression (0) | 2022.12.13 |
| [ML] Classification Algorithms –Decision Trees (2) | 2022.12.12 |





댓글 영역