고정 헤더 영역
상세 컨텐츠
본문
Decision Tree
1. Gini index
노드 t의 gini index를 구하는 공식은 아래와 같다.
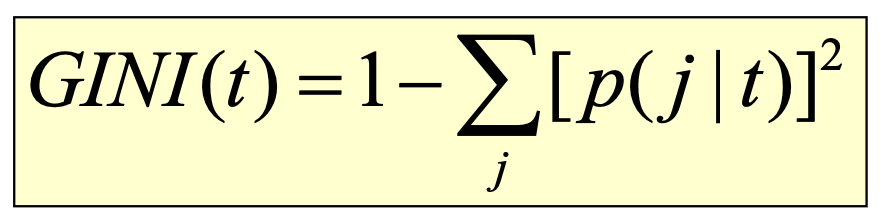
데이터가 모든 클래스에 균등하게 분포되어 있는 경우가 Gini index의 최대값을 갖는다. 그 최대값은 (1 - 1/nc)이다.
모든 데이터가 하나의 클래스에 속할 때는 Gini index의 최소값인 (0.0)을 갖는다.
아래 표에서 가장 왼쪽에 있는 경우가 Gini index의 최소값을 가지고 있고, 가장 오른쪽에 있는 경우가 Gini index의 최대값을 가지고 있다.

왼쪽부터 차례대로 Gini index를 구하는 과정은 다음과 같다.
<1>
P(C1) = 0/6 = 0
P(C2) = 6/6 = 1
Gini=1–P(C1)^2–P(C2)^2 =1–0–1=0
<2>
P(C1) = 1/6
P(C2) = 5/6
Gini = 1 – (1/6)^2 – (5/6)^2 = 0.278
<3>
P(C1) = 2/6
P(C2) = 4/6
Gini = 1 – (2/6)^2 – (4/6)^2 = 0.444
<4>
P(C1) = 3/6
P(C2) = 3/6
Gini = 1 – (3/6)^2 – (3/6)^2 = 0.5
Gini Decision Tree를 그림으로 나타낸 것이다. Gini index값이 0인 것은 트리의 leaf 노드이다.

이제 Gini index를 계산 했으면 Gini gain을 통해 어떤 split이 가장 좋은 것인지 판단해야 한다.
가장 좋은 split을 고르는 과정은 다음과 같다.

각 분할에 대해("A", "B")
▪ 분할하기 전에 노드에 대한 Gini index 계산 ("부모"): M0).
▪ 노드를 k개의 파티션으로 분할("A"의 경우 k=2, "B"의 경우 k=2).
▪ 각 파티션에 대해 Gini 계산("A"의 경우 M1 및 M2, "B"의 경우 M3 및 M4).
▪ k 파티션에 대한 가중 Gini 계산(M12, M34)
▪ Gini gain 계산
("부모"의 경우 Gini – k 파티션의 경우 가중치 Gini)
▪ 최대 Gini gain을 제공하는 분할 선택
weighted gini 를 계산하는 공식은 아래와 같다.

2. Naive Method (for Continuous Attribute)
◼ 하나의 분할 값을 기반으로 하는 이진 결정 사용 v
◼ 분할 가능한 값 수 = 구별되는 값의 수
◼ 최상의 V를 선택하는 간단한 방법
◼ 각 v에 대해 데이터 세트를 두 번 스캔하여 카운트 행렬을 수집하고 Gini 인덱스를 계산
=> 계산적으로 비효율적
Record = n, V (number of value) = n 이라고 할때,
navie method의 Scan = 2*n*n 이고,
계산 시간은 O(n^2)이다.
3. Efficient Method (for Continuous Attribute)
각 attribute에 대하여
◼ 특성 값을 정렬
◼ 이 값들을 순차적으로 스캔하여 매번 카운트 매트릭스와 Gini index 업데이트
◼ 인접한 두 속성 값 사이의 중간으로 분할 위치를 선택하고 각각에 대해 Gini index를 계산
◼ 최소 Gini index를 갖는 분할 위치 선택
Record = n, V (number of value) = n+1 이라고 할때,
efficient method의 Scan = n+1 이고,
계산시간은 O(n) 이다.
4. Classification error
노드 t의 classification error를 구하는 공식은 아래와 같다.

데이터가 모든 클래스에 균등하게 분포되어 있는 경우가 classification error의 최대값을 갖는다. 그 최대값은 (1 - 1/nc)이다.
모든 데이터가 하나의 클래스에 속할 때는 classification error의 최소값인 (0.0)을 갖는다.
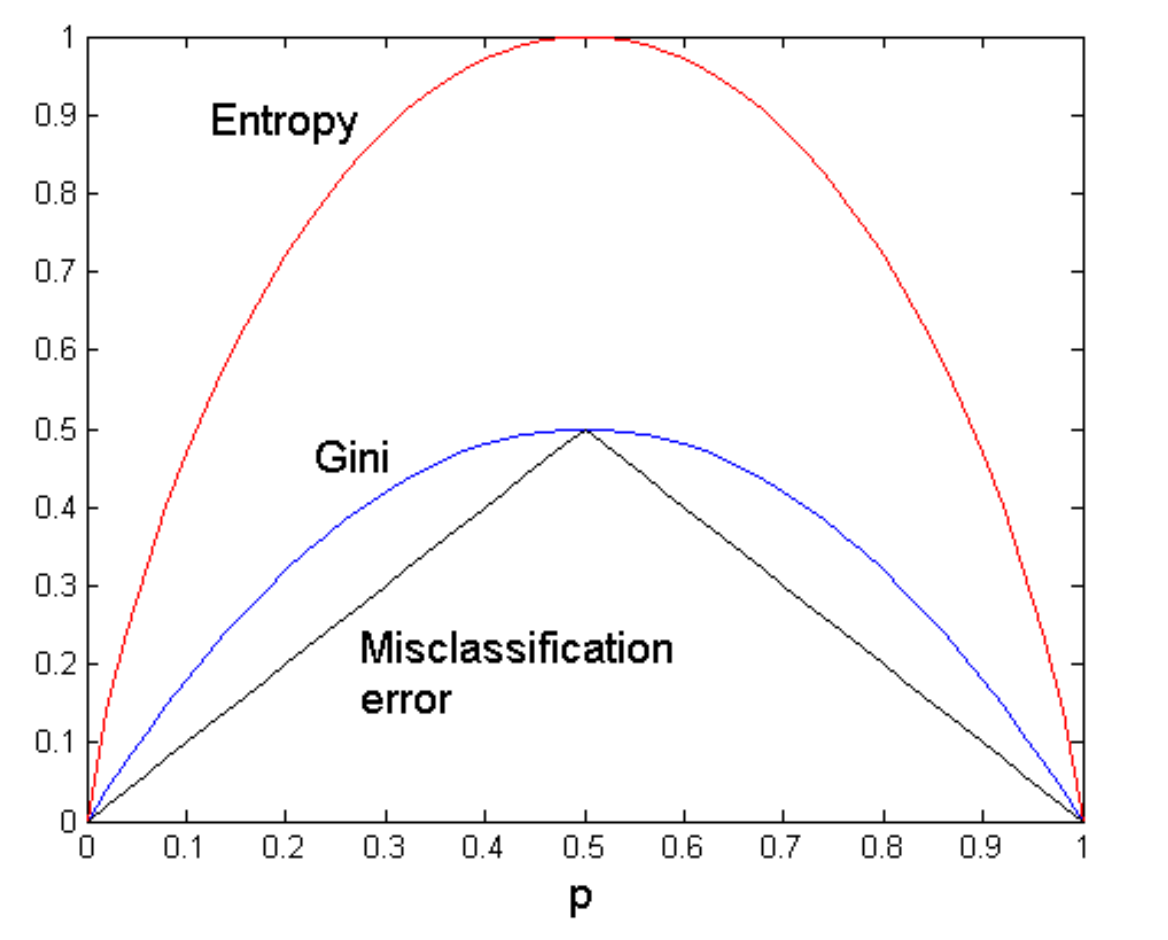
아래 그래프는 splitting 기준(entropy, gini, misclassification error)을 비교한 것이다.
entropy의 impurity는 gini의 impurity와 misclassification error보다 높다. 이것이 이론적으로 gini index가 entropy보다 나은 이유이다.
* Advantages of Decision Tree
◼ decision tree를 만드는데 비싸지 않다. (소규모 데이터셋의 경우)
◼ 알 수 없는 레코드를 빠르게 분류한다.
◼ 정확성이 비교적 좋다. 단순한 데이터 세트의 경우)
◼ 작은 크기의 나무를 해석하기 쉽다.
◼ 연속형 변수와 범주형 변수를 모두 처리할 수 있다.
◼ 분류 및 회귀 작업을 모두 처리할 수 있다.
◼ 앙상블 학습 모델의 기본값이다.(Random Forest, AdaBoost, Gradient Boost)
* Weakness of Decision Tree
◼ 클래스가 너무 많으면 오류가 발생하기 쉽다.
◼ training 비용이 많이 든다.(정렬, 속성 조합 등)
◼ Greedy 알고리즘(트리의 각 레벨에서 최선의 분할 결정을 내리고 다른 모든 결정은 삭제)
Decision Tree Regression
* Classification vs Regression
◼ Classification: 범주형 속성 예측
◼ Regression: 연속형 속성 예측
Pandas와 Scikit Learn을 사용한 Decision Tree Regression
from sklearn.model_selection import train_test_split from sklearn import datasets
from sklearn.tree import DecisionTreeRegressor
x_training_set, x_test_set, y_training_set, y_test_set = train_test_split(X,y,test_size=0.10,random_state=42, shuffle=True)
model = DecisionTreeRegressor(max_depth=5, random_state=0) model.fit(x_training_set, y_training_set)
Decision Tree Pruning
pruning은 모델에 포함할 가치가 없는 하위 트리 중 일부를 삭제하는 것을 의미한다. Decision tree에서 pruning의 목적은 트리 계산 비용을 제한하고 overfitting을 방지하기 위해서이다.
1. Pre-pruning (early stopping of tree induction)
일부 노드에서 하위 트리 구성을 중지하는 방법
◼ 레코드 수가 사용자가 지정한 임계값보다 작을 경우 중지
◼ 전류 노드를 확장해도 impurity 측정(Gini, information gain)이 개선되지 않으면 중지
2. Post-pruning (pruning the fully grown tree)
완전히 성장한 의사 결정 트리의 일부 노드를 상향식 또는 하향식으로 제거하는 방법
◼ 노드에서 하위 트리를 제거한 후 classification error가 더 심하지 않으면 하위 트리를 leaf 노드로 교체
'machine learning' 카테고리의 다른 글
| [ML] Clustering Algorithms –Expectation-Maximization (Gaussian Mixture Model) (0) | 2022.12.15 |
|---|---|
| [ML] Clustering Algorithms – Partitioning (0) | 2022.12.15 |
| [ML] Clustering Algorithms – Clustering Quality Measure (2) | 2022.12.14 |
| [ML] Classification Algorithms – Support Vector Machine (0) | 2022.12.13 |
| [ML] Classification Algorithms – Logistic Regression (0) | 2022.12.13 |





댓글 영역