고정 헤더 영역
상세 컨텐츠
본문
Regularization
정규화는 과적합 위험을 최소화하기 위해 비용 함수의 매개 변수를 제한하는 것을 목표로 한다. 선형 회귀 분석, 로지스틱 회귀 분석 및 딥 러닝에 사용할 수 있습니다. 이번에는 선형 회귀에 사용되는 함수를 보여줄 것이다.
회귀 모형을 개선하는데는 두 가지 방법이 있다.
◼ 분산을 줄임으로써 예측 정확도를 향상시킨다.
◼ 모든 feature를 사용하는 대신 독립 변수(feature)의 관련 부분 집합을 선택하여 모델 해석성을 향상시킨다.
결정 계수 R^2의 값이 높을수록 정확도가 높다. R^2은 회귀 분석(SSR)으로 설명되는 총 변동(SST)의 비율(백분율)로 아래와 같이 구할 수 있다.

하지만 R^2은 문제가 있다. 예측 변수가 추가되면 R^2가 증가하거나 일정하게 유지되지만 절대 감소하지는 않는다.
이러한 문제를 해결하기 위한 Adjusted R^2은 모형의 예측 변수 수(즉, 자유도)를 설명한다.

여기서 p는 예측 변수의 수이고, N은 표본의 총 개수입니다.
Adjusted R^2는 새 예측 변수가 모형 정확도를 향상시키는 경우에만 증가한다. 그러나 수정된 R^2 통계량에는 모형에 불필요한 변수가 포함되어 있다. 정규화는 이러한 Adjusted R^2의 문제를 개선하기 위한 것이다.
1. Ridge Regression
◼ 회귀 모델의 비용 함수(최소화할 것)에 페널티 항을 추가하여 β 매개변수를 강제로 감소시킨다.
◼ 패널티 항에 L2(squared Euclidean norm)를 사용한다.
◼ Ridge regression은 약간 다른 양을 최소화하여 β 계수를 추정한다는 점을 제외하고 OLS와 유사하다.
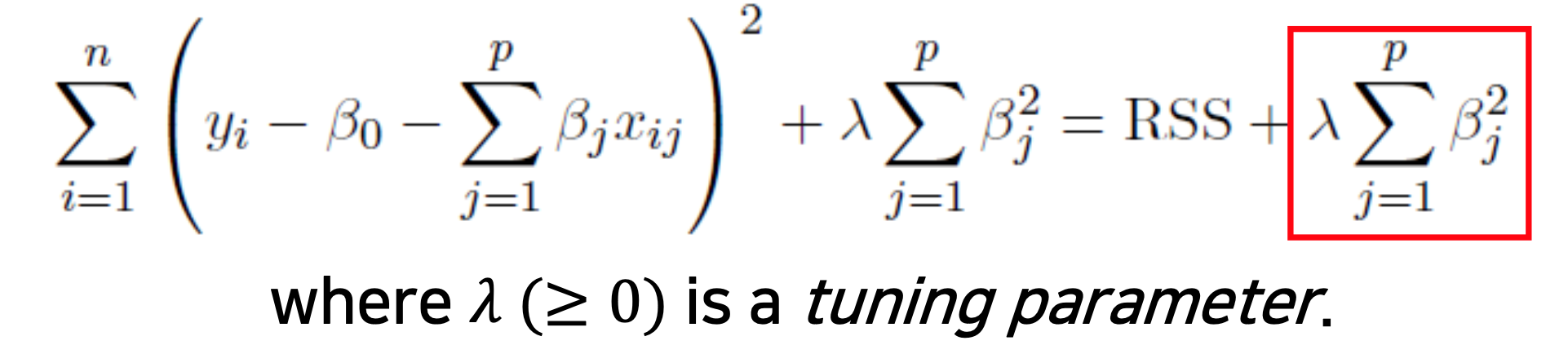
아래 그림은 Lambda의 크기에 따른 변화를 보여준다.

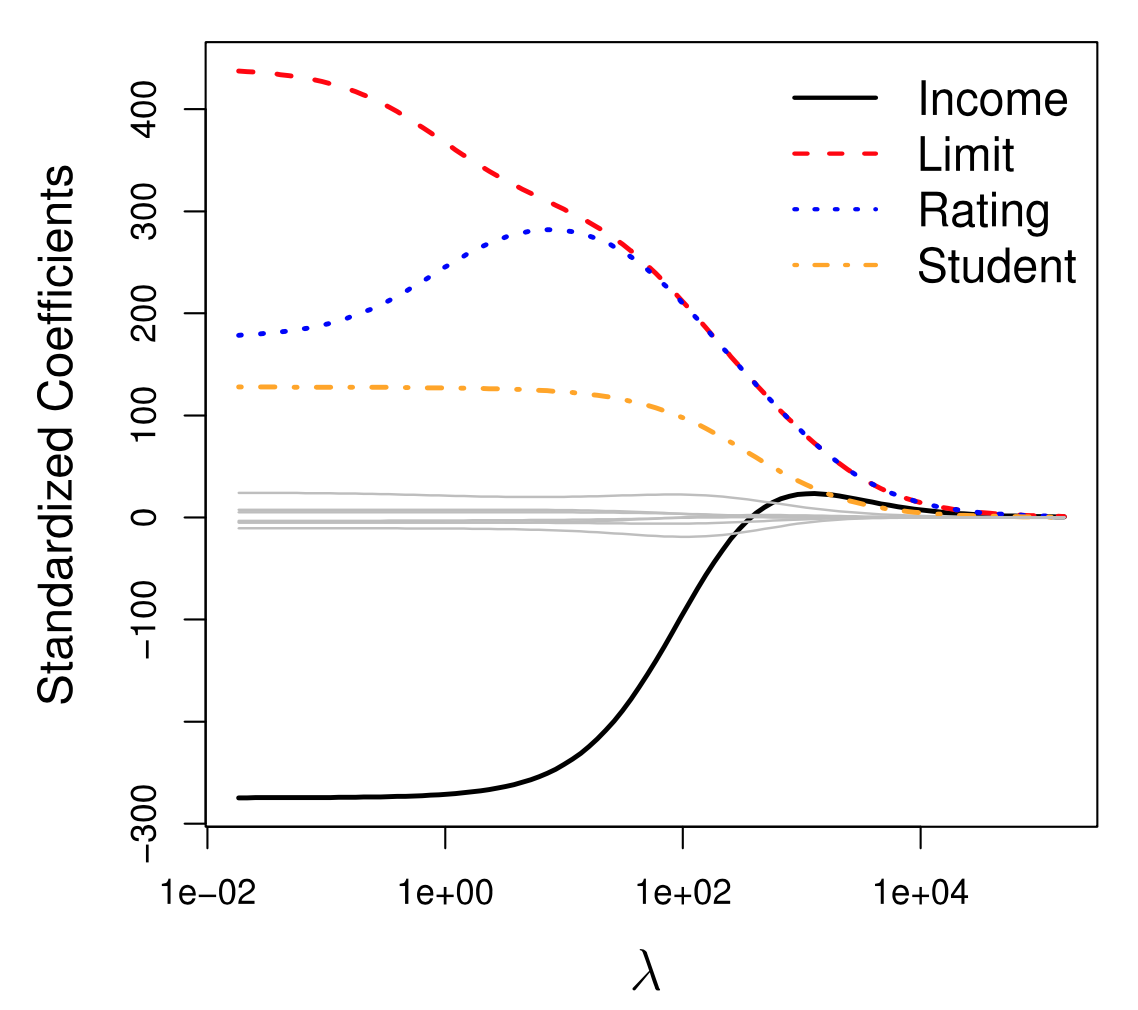
정규화를 위해서는 좋은 Lambda값을 선택하는 것이 중요하다. Lambda는 Ridge regression의 hyperparameter이며 cross-validation을 통해서만 확인할 수 있다.
아래 그림을 보면 Lambda가 증가하면 표준화된 Ridge regression coefficients가 0에 가까워진다.
Ridge regression에서는 스케일링의 필요성이 더 강하다. 이는 Ridge regression 비용 함수의 패널티 부분에 있는 계수 항 제곱의 합으로 인해 주어진 예측 변수에 상수를 곱할 때 Ridge regression계수 추정치가 크게 변경될 수 있기 때문아다.
따라서 다음과 같이 예측 변수를 표준화한 후 Ridge regression을 적용하는 것이 가장 좋다.
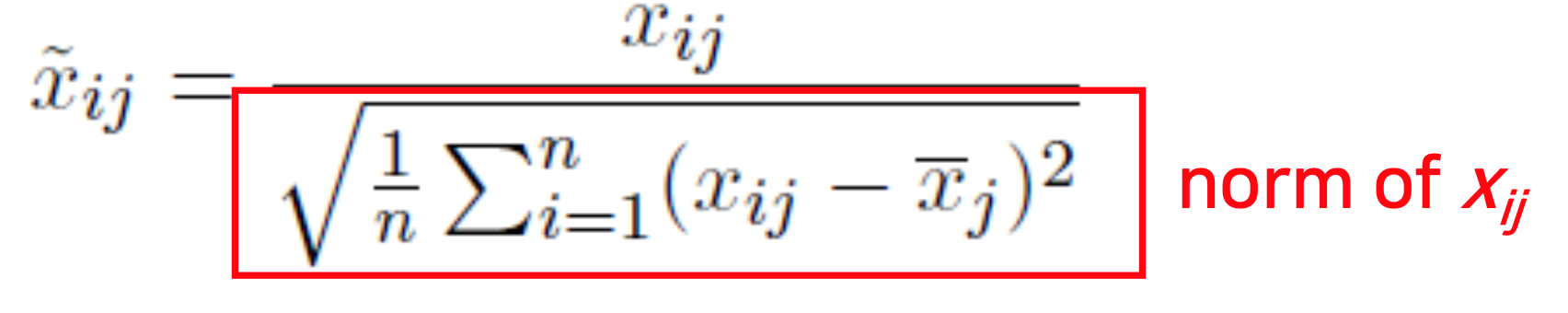
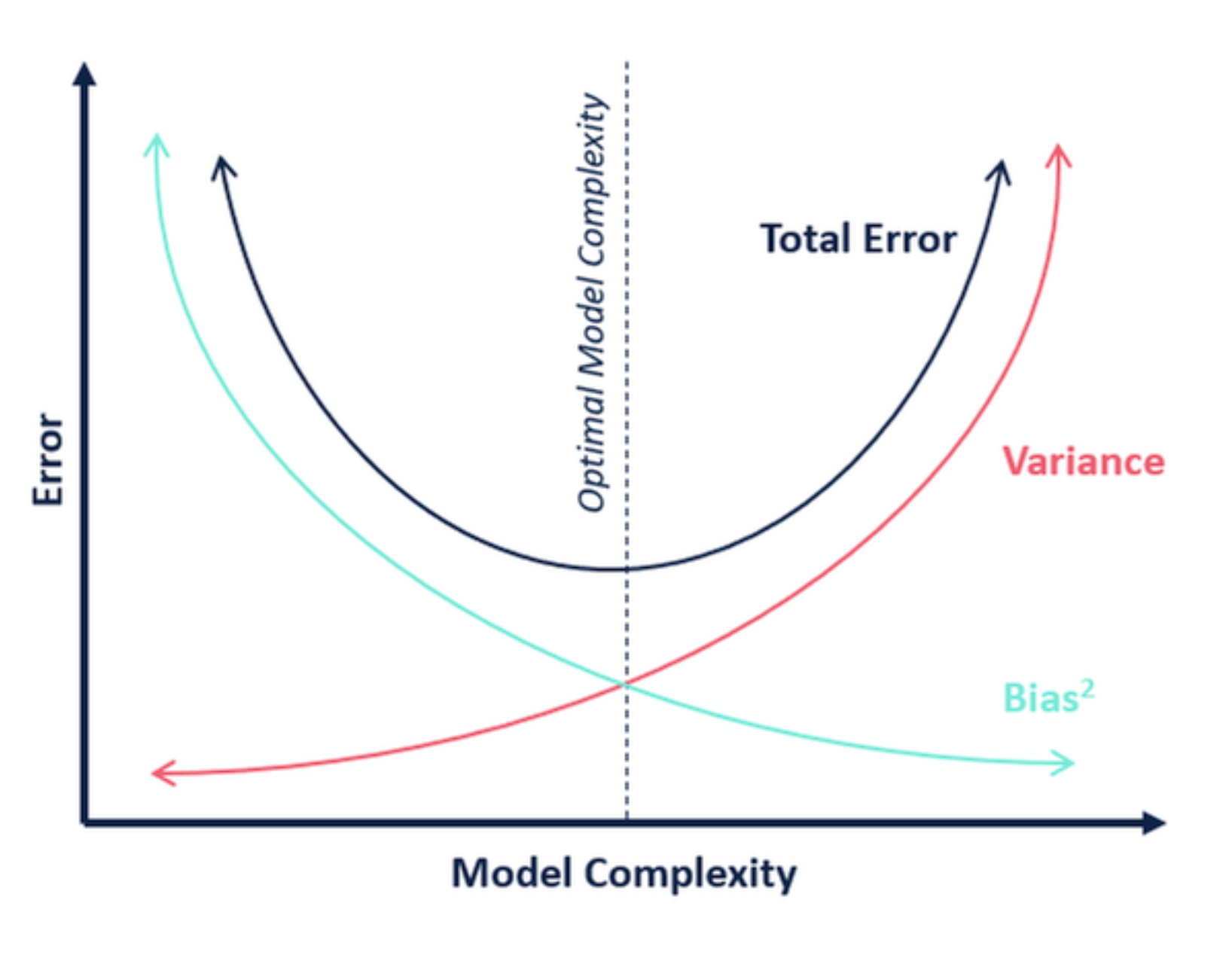
penalty term은 Ridge regression 추정치를 편향되게 만들지만 분산을 상당히 줄일 수도 있다. 결과적으로 bias/variance tradeoff가 발생한다.
-Python code for Ridge Regression
# Setting up: Import libraries import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Loading data
DATAPATH = ‘data/Advertising.csv’
Data = pd.read_csv(DATAPATH)
Data.head()
# Take out the useless Unnamed:0 column
Data.drop([‘Unnamed: 0’], axis=1, inplace=True)
Data.head()
# Multiple linear regression, with least squares fitting
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
x5 = data.drop([‘sales’], axis=1)
y = data[‘sales’].values.reshape(-1,1)
lin_reg = LinearRegression()
MSE5 = cross_val_score(lin_reg, x5, y, scoring=‘neg_mean_squared_error’, cv=5)
mean_MSE = np.mean(MSE5)
print(mean_MSE)
# GridSearchCV allows us to automatically perform 5-fold cross validation with a range of different regularization parameters in order to find the optimal value of alpha.
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import Ridge
ridge = Ridge()
parameters = {‘alpha’: [1e-15, 1e-10, 1e-8, 1e-4, 1e-3, 1e-2, 1, 5, 10, 20]}
ridge_regressor = GridSearchCV(ridge, parameters, scoring=‘neg_mean_squared_error’, cv=5)
ridge_regressor.fit(x5, y)
# find the best parameter and the best MSE
print(ridge_regressor.best_params_)
print(ridge_regressor.best_score_)
# The optimal value of alpha is 20, with a negative MSE of -3.07267.
# This is a slight improvement upon the basic multiple linear regression.-Limitation of Ridge Regression
◼ 모든 예측 변수를 유지하므로 모형을 해석하고 계산하기가 복잡하다.
2. LASSO(Least Absolute Shrinkable Selector Operator) Regression
◼ L1(absolute norm) 정규화 기법을 사용한다.
◼ LASSO는 수량을 최소화한다.
◼ Ridge 회귀 분석과의 주요 차이점은 LASSO가 L2 대신 L1 패널티를 사용하고, 튜닝 매개 변수 λ가 충분히 클 때 일부 계수를 0과 동일하게 만든다는 것이다.
◼ LASSO는 feature selection을 수행한다.

아래 그림을 보면 λ = 0일 때 LASSO = OLS이다. λ가 충분히 커지면 LASSO는 모든 계수 추정치가 0인 null 모형을 제공한다.
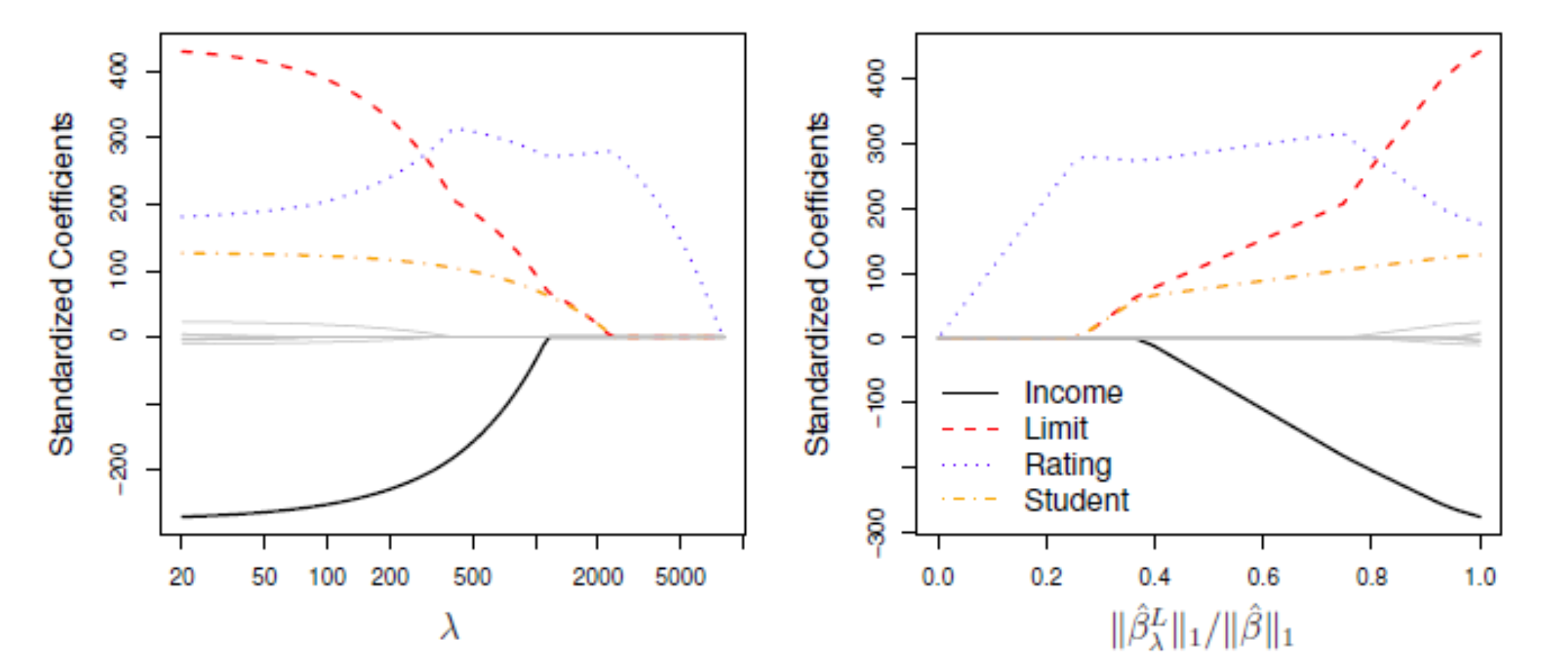
- Lasso vs Ridge Regression
◼ LASSO는 예측 변수의 하위 집합만 포함하는 더 단순하고 해석 가능한 모형을 생성한다는 점에서 Ridge Regression에 비해 큰 이점이 있다.
◼ LASSO는 Ridge Regression에 비해 더 정확한 예측을 생성할 수 있다.
◼ LASSO와 Ridge는 λ가 증가할수록 분산이 감소하고 치우침이 증가한다는 점에서 질적으로 유사한 거동을 보인다.
◼ Cross-validation을 사용하여 특정 데이터 세트에서 어떤 접근 방식이 더 나은지 결정할 수 있다.
-Python code for LASSO
from sklearn.linear_model import lasso
lasso = Lasso()
parameters = {‘alpha’: [1e-15, 1e-10, 1e-8, 1e-4, 1e-3, 1e-2, 1, 5, 10, 20]}
lasso_regressor = GridSearchCV(lasso, parameters, scoring=‘neg_mean_squared_error’, cv=5)
lasso_regressor.fit(x5, y)
# find the best parameter and the best MSE
print(lasso_regressor.best_params_)
print(lasso_regressor.best_score_)
# The optimal value of alpha is 1, with a negative MSE of - 3.0414.
# This is the best score of all three models.-Limitation of LASSO
◼ "큰 p, 작은 n" 경우(p 변수 및 n 관측치)(예: 이미지 데이터)에서 LASSO는 포화되기 전에 최대 n개의 변수를 선택한다.
◼ LASSO는 상관성이 높은 변수의 그룹이 있을 경우 그룹에서 하나의 변수만 선택하고 다른 변수는 모두 무시하는 경향이 있다. 이로 인해 정보가 일부 손실되어 모델의 정확도가 낮아질 수 있다.
3. Elastic Net Regression
◼ L1 및 L2 패널티 조건을 모두 사용한다.
◼ 패널티를 결합하면 관측치 수(n)보다 더 많은 예측 변수(p)를 선택할 수 있다.
◼ LASSO와 달리 Elastic net은 상관 변수 그룹을 형성하고 그룹의 변수 중 하나가 강력한 예측 변수인 경우 모형에 대한 전체 그룹을 선택한다.
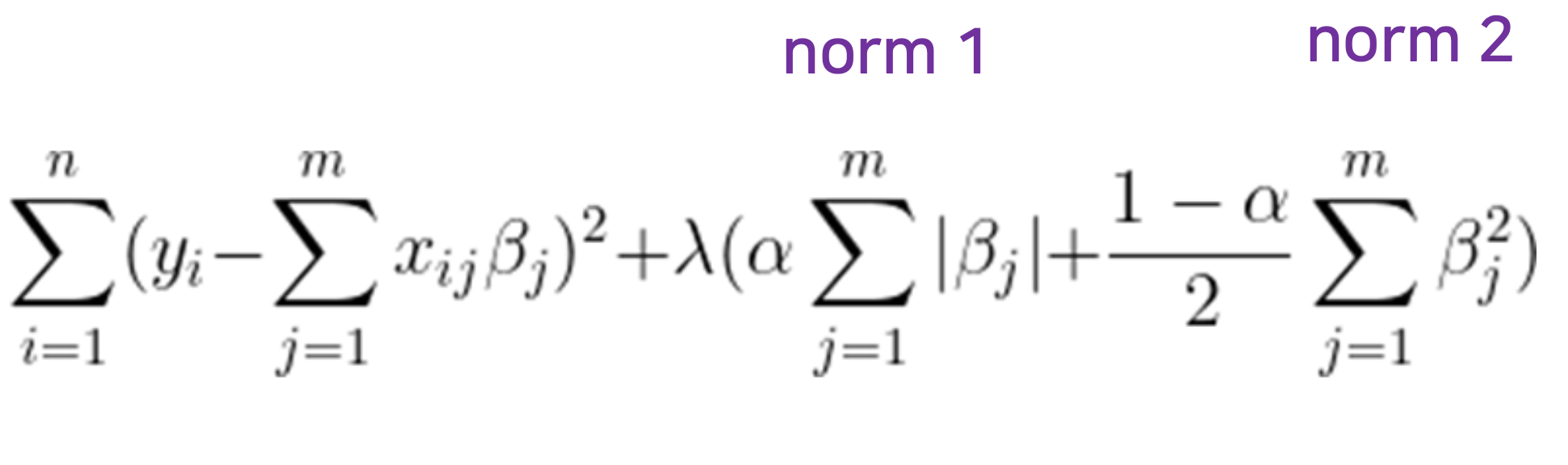
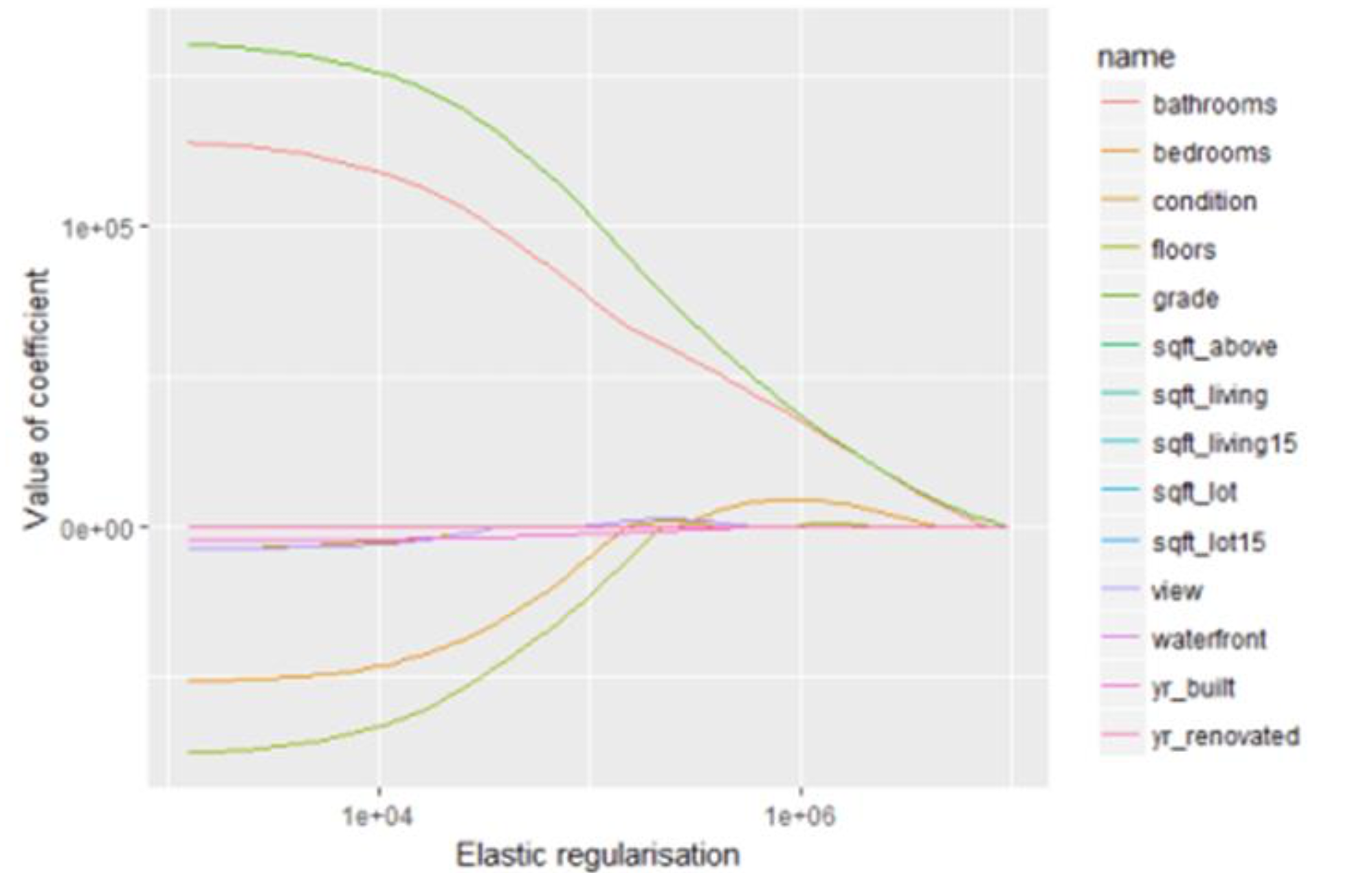
아래 그림은 Shrinkage Term과 Elastic Net의 관계를 보여준다.
'machine learning' 카테고리의 다른 글
| [ML] Bayesian Classifier and Markov Model (0) | 2022.12.20 |
|---|---|
| [ML] Cost Function Optimization – Gradient Descent (0) | 2022.12.17 |
| [ML] Classification - SMOTE (0) | 2022.12.16 |
| [ML] Clustering Algorithms – DBSCAN (0) | 2022.12.15 |
| [ML] Clustering Algorithms –Expectation-Maximization (Gaussian Mixture Model) (0) | 2022.12.15 |





댓글 영역