고정 헤더 영역
상세 컨텐츠
본문
Bayesian Classifier
◼ 통계적 분류방법
◼ 지도 학습 방법
◼ Bayes’ rule을 기본 확률 모델로 가정
- Elements of Bayesian Classifier
◼ D: 튜플(샘플) 집합 X
◼ X: n차원 속성 벡터 {x1,x2,x3,...,xn} (여기서 xi는 Ai 특성의 값)
◼ m 클래스: C1, C2, C3, ..., Cm
◼ Maximum a Posteriori (MAP) Rule: P(X)가 상수일때 아래 공식에서 분자값을 최대화
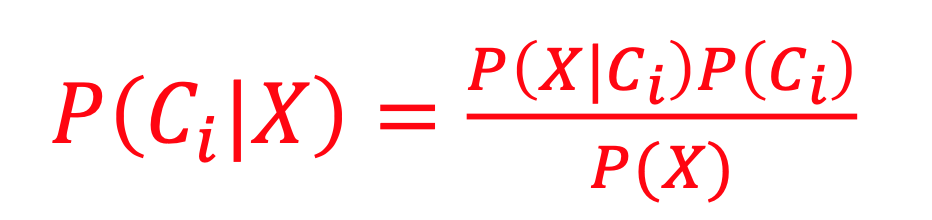
Naïve Bayesian Classifier
◼ 일반적으로 일부 변수(feature 또는 독립 변수)는 원인에 따라 달라질 뿐만 아니라 서로 종속된다.
◼ 그러나 종속성 그래프가 깊어질수록 조건부 확률 테이블은 다루기 어려울 정도로 커진다.
◼ Naïve Bayes Model은 원인이 주어진 증상의 독립성을 가정한다.
◼ Naïve Bayes는 추론을 더 쉽게 만드는 베이지안 네트워크의 특별한 경우이다.
◼ 큰 n(즉, 특징의 수)을 사용하면 P(X┃Ci)를 평가하는 데 비용이 많이 든다.
◼ 클래스 조건을 독립적이라 가정하다.

- walkthrough example
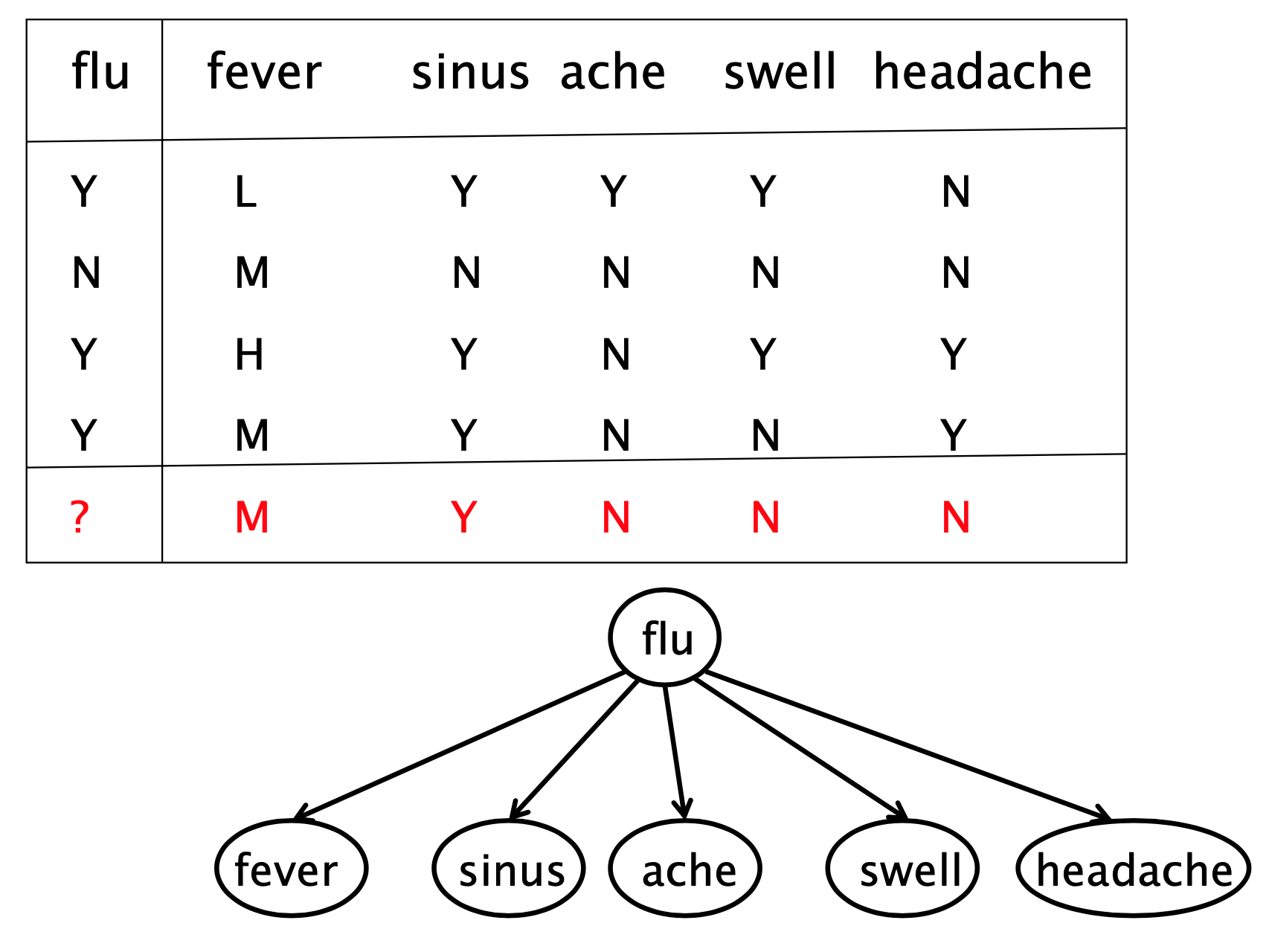
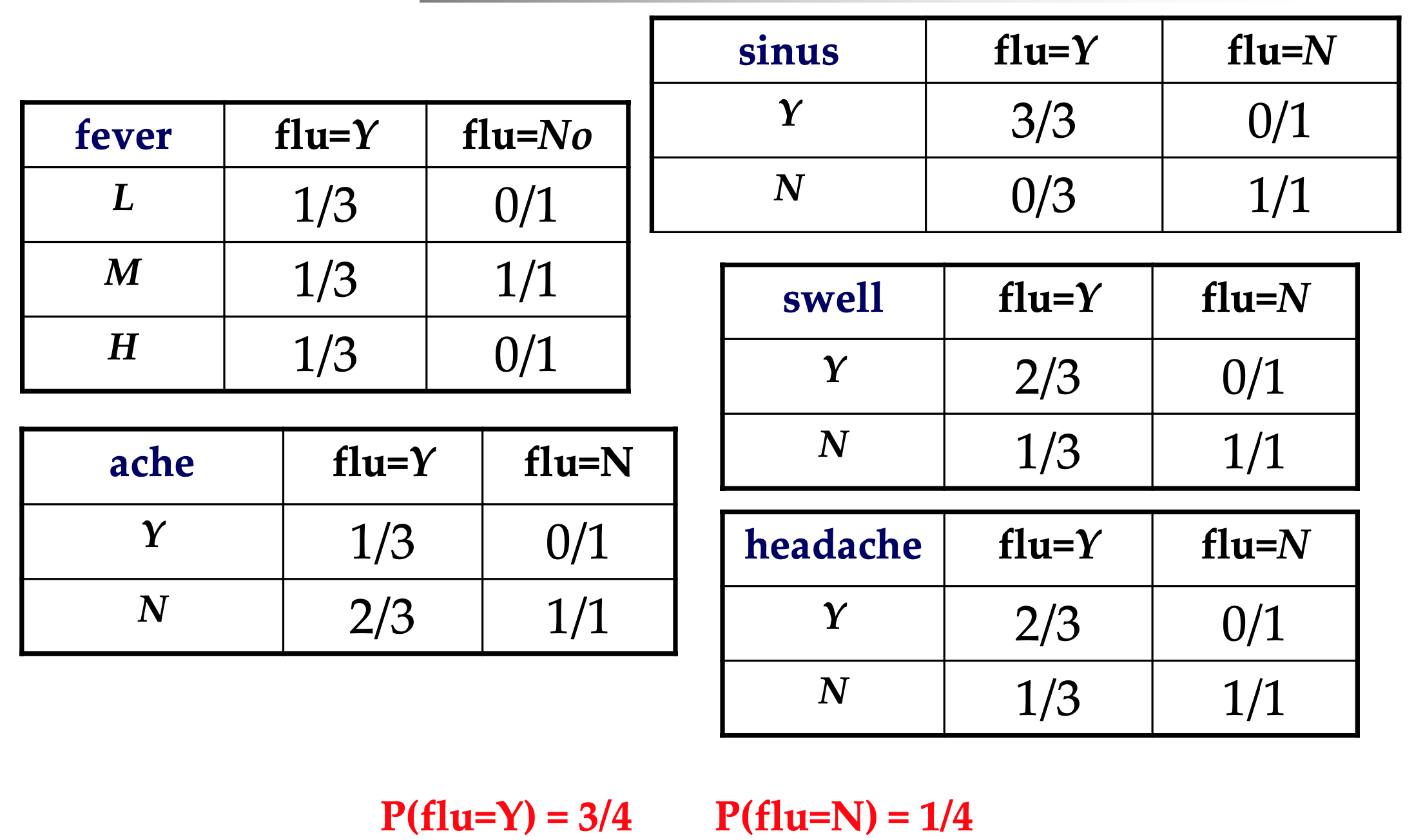

*Laplace correlation
형상이 많은 모형이 있는 경우 형상 값 중 하나가 0이면 전체 확률이 0이 될 수 있다. 이를 방지하기 위해, 우리는 전체 확률이 0이 되지 않도록 분자의 값이 0인 변수의 카운트를 작은 값(보통 분자가 큰 경우 1)으로 늘린다.
- Advantages of Naïve Bayes
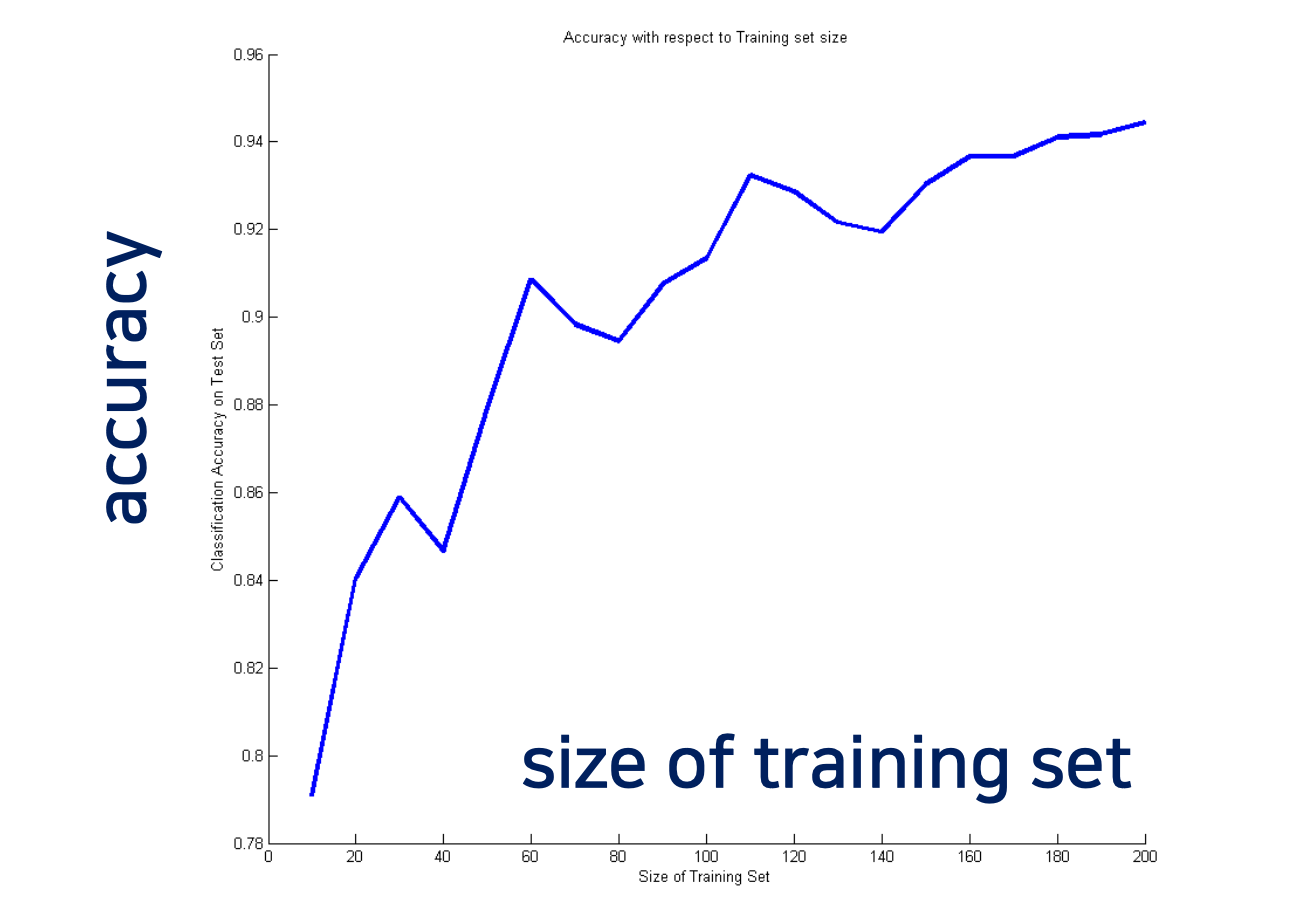
◼ 알고리즘이 예측 결과에 얼마나 자신감이 있는지 알려주는 확률을 반환한다.
◼ 구현이 쉽고 소규모 training dataset에 적합한 경우가 많다.
- Python code
# Assigning features and label variables
weather=['Sunny','Sunny','Overcast','Rainy','Rainy','Rainy','Overcast',' Sunny','Sunny', 'Rainy','Sunny','Overcast','Overcast','Rainy']
temp=['Hot','Hot','Hot','Mild','Cool','Cool','Cool','Mild','Cool','Mild','Mild', 'Mild','Hot','Mild']
play=['No','No','Yes','Yes','Yes','No','Yes','No','Yes','Yes','Yes','Yes','Yes' ,'No']
# Import LabelEncoder
from sklearn import preprocessing
#create labelEncoder
le = preprocessing.LabelEncoder()
# Convert string labels into numbers.
wheather_encoded=le.fit_transform(wheather)
print wheather_encoded
temp_encoded=le.fit_transform(temp) label=le.fit_transform(play)
print "Temp:",temp_encoded
print "Play:",label
features=zip(weather_encoded,temp_encoded)
print features
#Import Gaussian Naive Bayes model
from sklearn.naive_bayes import GaussianNB #Create a Gaussian Classifier
model = GaussianNB()
# Train the model using the training sets
model.fit(features,label)
#Predict Output
predicted= model.predict([[0,2]]) # 0:Overcast, 2:Mild
print "Predicted Value:", predicted
Markov Model
◼ 확률 분포가 현재 상태에 의해서만 결정되는 랜덤 시퀀스이다.
◼ 관측 가능한 상태 시퀀스(상태는 데이터에서 알 수 있음)는 Markov chain model로 이어진다.
◼ 관찰할 수 없는 상태는 Hidden Markov Model(HMM)로 이어진다.
- Markov의 속성
시간 t+1의 시스템 상태는 시간 t의 시스템 상태에만 의존한다.
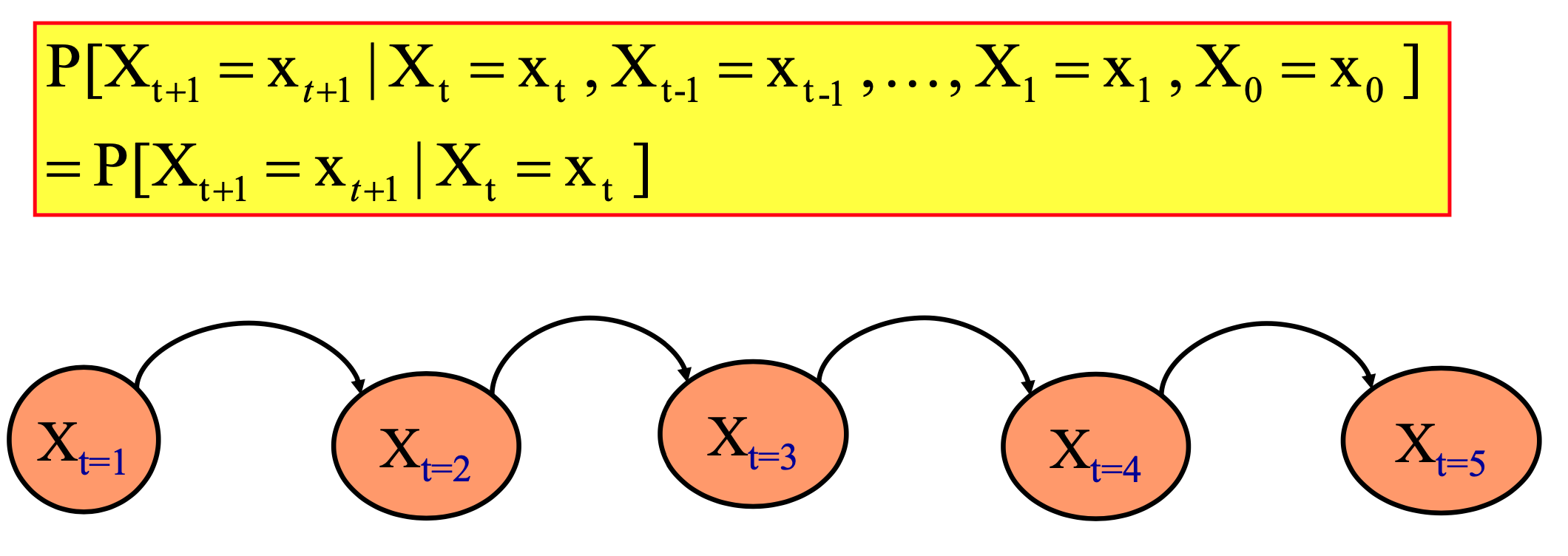
- Markov chain/model
◼ 이산(유한) 시스템:
◼ N개의 별개 상태
◼ 일부 초기 상태에서 시작(시간 t=1)
◼ 각 시간 단계(t=1,2,...)에서 시스템은 현재 상태와 관련된 전환 확률에 따라 현재 상태에서 다음 상태로 이동
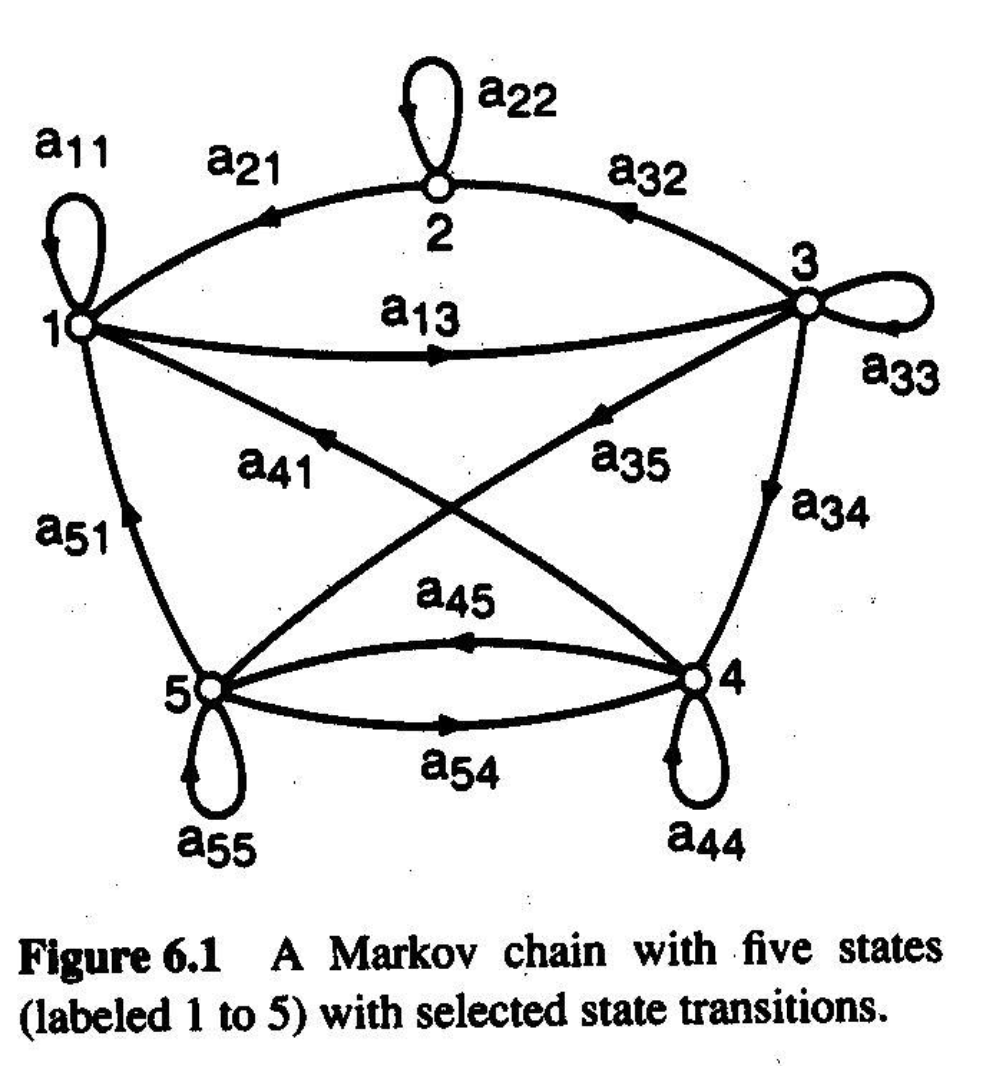
◼ 위 그림에서 각 aij는 상태 i에서 상태 j로 이동할 확률을 나타낸다.
◼ aij는 행렬 A = {aij}에 주어진다.
◼ 주어진 상태 i에서 시작할 확률은 pi이다. 벡터 p는 이러한 시작 확률을 나타낸다.

아래 matrix는 위 그림을 Transition matrix (stochastic matrix)로 변환한 것이다.

* 참고: 각 행의 합계는 1이다.
- Example
강세(bull) 주간은 90%, 약세(bear) 주간은 7.5%, 정체(stagnant) 주간은 2.5%이다. {1 = bull, 2 = bear, 3 = stagnant}
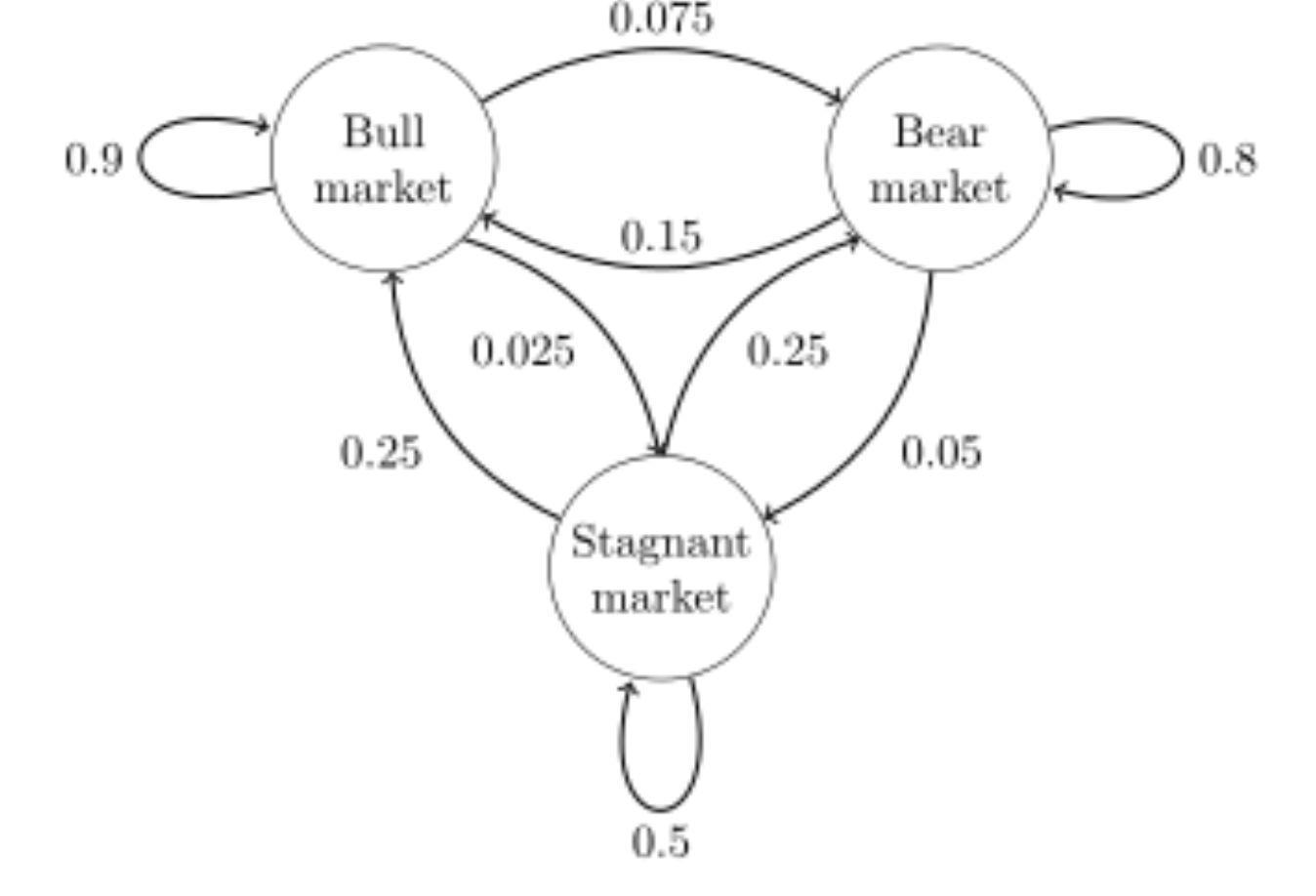
Transition matrix를 구하면 아래와 같다.

만약 시간 n에서 시스템이 상태 2(bear)에 있다면, 세 시간 후에 시간 n + 3에서 확률 분포는 다음과 같다.

Hidden Markov Model
◼ discrete Markov model은 신호를 방출하는 일련의 상태를 통과한다.
◼ "방출 신호"는 단순히 "일부 데이터 전송"을 의미하다.
◼ 신호 시퀀스에서 상태 시퀀스를 결정할 수 없는 경우 모델을 Hidden Markov model이라고 한다.

Bayesian Networks
◼ DAG(방향 비순환 그래프)를 통해 랜덤 변수 집합과 조건부 종속성을 나타내는 통계 모델의 한 유형이다.
◼ 예를 들어 Bayesian network는 질병과 증상 사이의 확률적 관계를 나타낼 수 있다. (증상이 주어지면 네트워크를 사용하여 다양한 질병의 존재 확률을 계산할 수 있다.)
- Conditional Probability Tables
◼ 각 노드는 노드의 상위 변수에 대한 특정 값 집합을 입력으로 취하고 노드에 의해 표현되는 변수의 확률(또는 확률 분포)을 출력으로 제공하는 확률 함수(표)와 연관된다.
◼ 베이지안 네트워크에 대한 일련의 조건부 확률 테이블이 있다.
◼ 베이지안 네트워크의 각 노드 Xi에는 노드에 대한 부모의 영향을 정량화하는 조건부 확률 분포 P(Xi┃ 부모(Xi))가 있다.
◼ 모수는 이러한 조건부 확률표(CPT)의 확률이다.
◼ 예를 들어, 부모 노드가 부울 변수를 나타내는 경우, 확률 함수는 부모의 가능한 각 조합에 대해 하나의 항목인 항목 테이블로 표현될 수 있다.

'machine learning' 카테고리의 다른 글
| [ML] Recommender Systems (0) | 2022.12.21 |
|---|---|
| [ML] Association Rules Discovery Algorithms (0) | 2022.12.21 |
| [ML] Cost Function Optimization – Gradient Descent (0) | 2022.12.17 |
| [ML] Cost Function Optimization - Regularization (0) | 2022.12.17 |
| [ML] Classification - SMOTE (0) | 2022.12.16 |





댓글 영역